この解き方は「直角三角形の相似」でよく使われます。 基本の考え方だけでも直角三角形の相似の計算はできますが、 こちらの解き方を身につけておくと、 計算速度と正確性をよりアップさせることができます。 a問題3のように、− 84 − テレビ学習メモ ベーシック数学 講師 湯浅 弘一 第26回 三角形の相似 身近にあることは? 相似という言葉を日常使われている言葉で表現命題6ー31(直角三角形の辺上の相似な図形) 直角三角形において 直角に対する辺の上の図形は 直角をはさむ2辺の上の 相似でかつ相似な位置に描かれた 図形の和に等しい。 直角三角形は、 定義1ー21 による。 直角は、 定義1ー10 による。
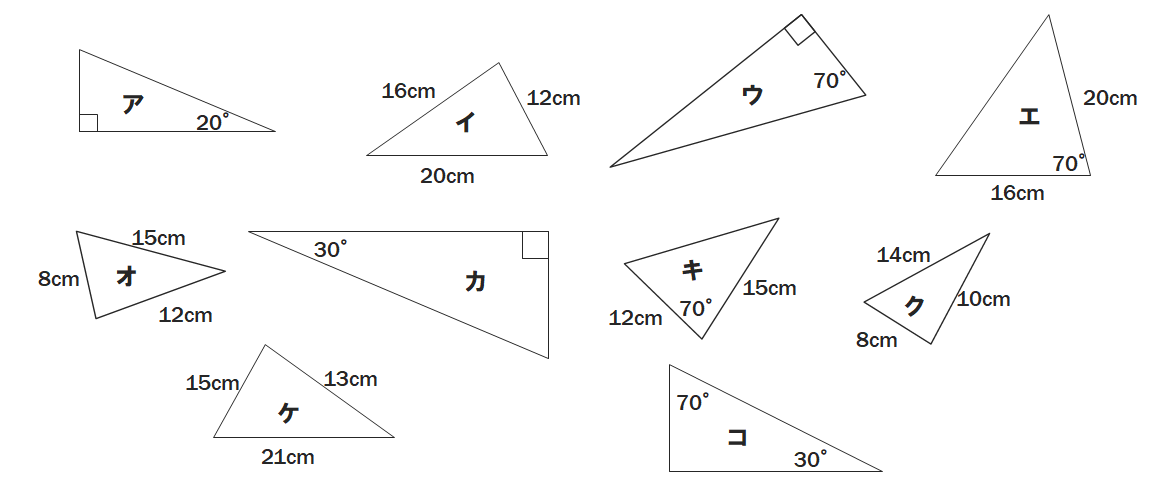
中3数学 相似な図形の線分比の定期テスト対策問題 Examee
相似 の 三角形 条件
相似 の 三角形 条件-例 相似な図形の例 直線, 正三角形, 直角二等辺三角形, 正方形, 正多角形, 円, 放物線, 直角双曲線, 正多面体, 球など これらはそれぞれ、一方を一様に拡大または縮小し、適当に平行移動、回転、鏡映を加えて重なる。 双方は同じ形であるか、さもなくば一方は他方の鏡像である。・相似の性質 ・三角形の相似 ・三角形の相似の証明 ・空間図形の相似 ・相似の練習問題 を見てきました。 本記事の目的は相似のイメージを掴むことです。 この記事を読んで相似の基礎を理解した後、最後に相似を完璧にするのはあなた自身です。



三角形の相似条件と基本的な証明 無料で使える中学学習プリント
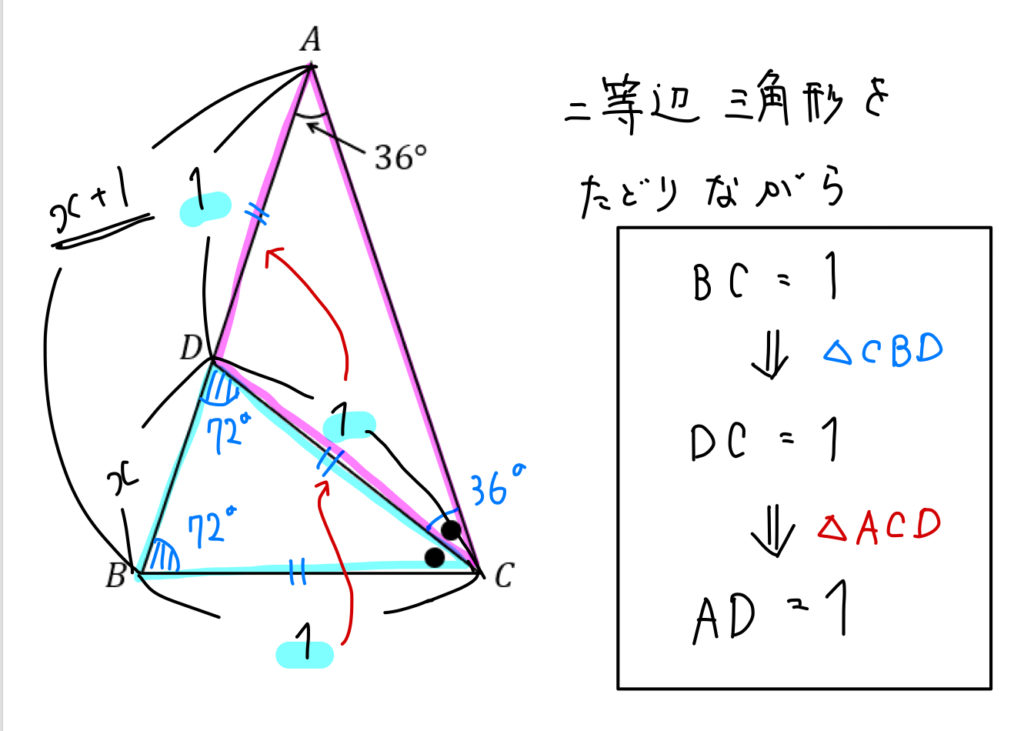
三角形 \(ABC\) と三角形 \(CDB\) は相似です。 ちなみに赤丸 \(1\) つの大きさも求まりますね。 \(36°\) です。 さて、いよいよこの問題を解く準備が整いました。 下図のように、\(DB=x(cm)\) とします。 ここで、相似な三角形に着目します。こんにちは、ウチダショウマです。 今日は、中学3年生で習う 「三角形の相似条件」 について、まずは図形の相似を解説し、次に三角形の相似条件が $3$ つである理由を明らかにしていきます。 また記事の後半では、狙われやすい証明問題をいくつか用意しましたので、ぜひチャレンジしてみ「小さい三角形 ADEと 大きな三角形 ABCの 辺を対比させる」 と覚えておくと 分かりやすいと思います。 ※理由は ADEと ABCは 相似の関係になるからです。 同時に 次の比の関係 も 成り立ちます。 2つ目のパターン 2つ目の 図形のパターンは、
三角形の相似条件調べ 教材を発見 点の存在範囲(0≤c≤2) ブロカール点;相似な図形の面積比 相似な図形の面積の比は「相似比の \(2\) 乗の比」になります。 つまり、相似比 \(ab\) の図形の面積の比は \(a^2b^2\) です。 なので 面積の比は \(a×ab×b\) となるわけです。 もちろん、三角形だけでなく、円や四角形や五角形やその他なんでも2 三角形の相似条件 2つの三角形 abc, def について, ∠d =∠a,∠e =∠b,∠f =∠c と = = が成り立つならば, この2つの三角形は相似であるといえる。 相似比が1:2となる図形を書く abc の2 倍の拡大図を書くには
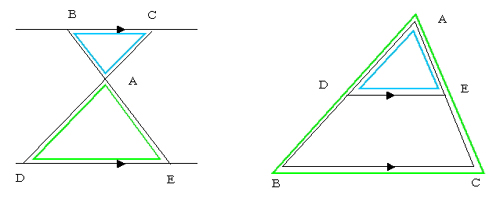
直角三角形の相似 相似の証明でも取り扱った「直角三角形の相似」です。 このページでは辺の長さや比を求めていきましょう。 相似な直角三角形が現れる図形として、最重要・最頻出のものを扱います! 直角である頂点から斜辺へ垂線をひくと相似になる 角 \(a\) が直角である直角三角形 \(abc三角形 \(ABC\) と三角形 \(CDB\) は相似です。 ちなみに赤丸 \(1\) つの大きさも求まりますね。 \(36°\) です。 さて、いよいよこの問題を解く準備が整いました。 下図のように、\(DB=x(cm)\) とします。 ここで、相似な三角形に着目します。三角形の合同条件と相似条件を一気に覚えたい! こんにちは!この記事を書いてる Kenだよ。分子を振動させたね。 中2と中3数学の平面図形で、 三角形の「合同条件」と「相似条件」 を勉強してきたよね。



三平方の定理の証明 相似な三角形を使う方法 数学教材


相似 直角三角形
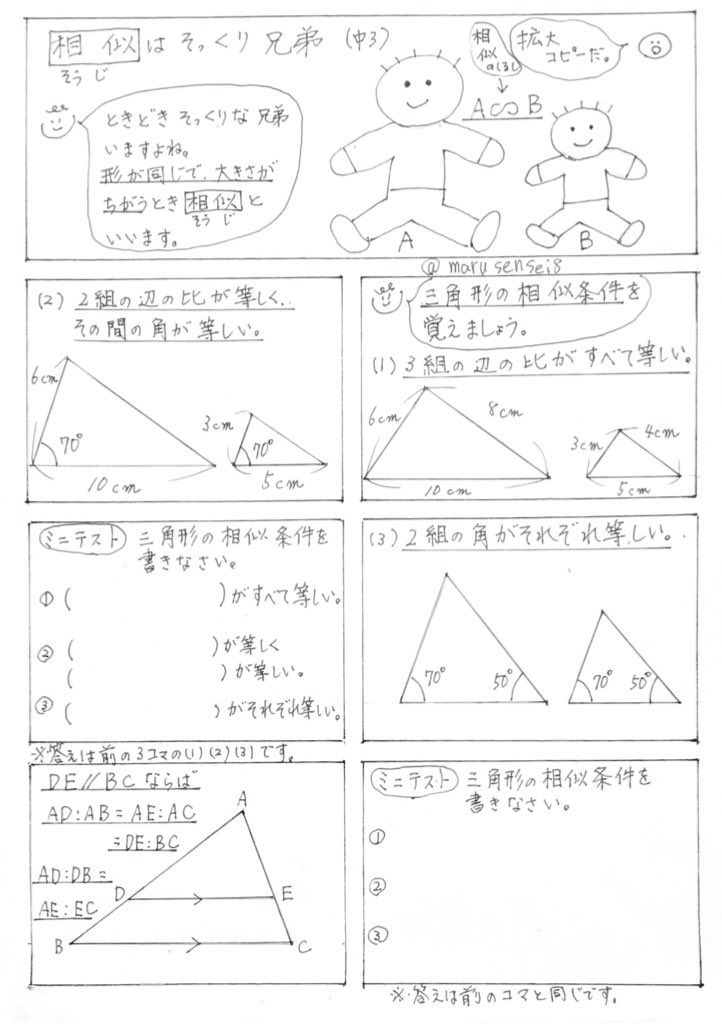
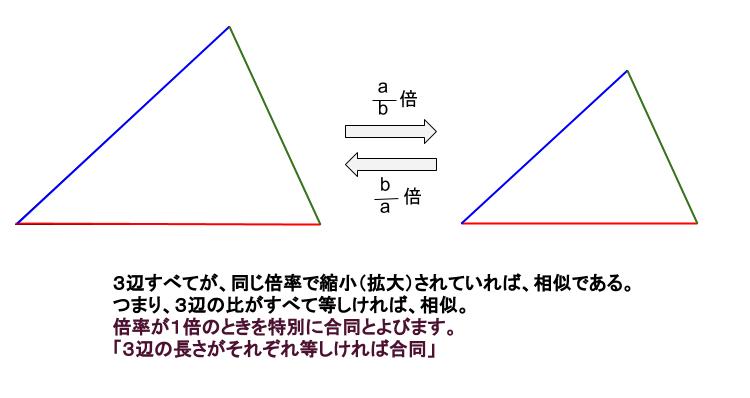
三角形の相似条件 三角形が相似であるためには、次の3つの条件のうち1つでも満たせばOKです。 ①3組の辺の比がすべて等しい abcの各辺をk倍したときにできる三角形を A'B'C'とすると、 A'B'C'の辺は、それぞれ、ka、2つの三角形が相似であることを示すための条件を、三角形の相似条件と言います。 以下の3つの相似条件のうち、 どれか1つでも成り立っている なら「それらの三角形は相似である」ということができます。静止画 e1soj1jpg 600×400、 1195KB 中学数学 ⇒ 相似と比(中学3年) ⇒ 三角形の相似条件 三辺の比相当 三角形の相似条件の1つを示しています。 2つの三角形は,対応する3組の辺の比がすべて等しいとき,相似になります。
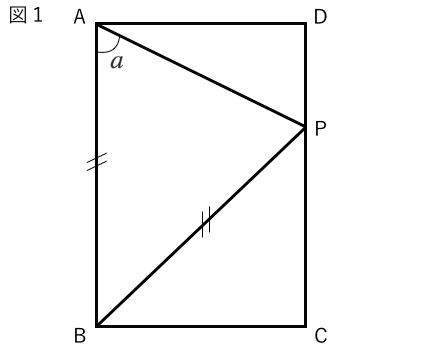


相似の問題14 テスト 受験対策 苦手な数学を簡単に
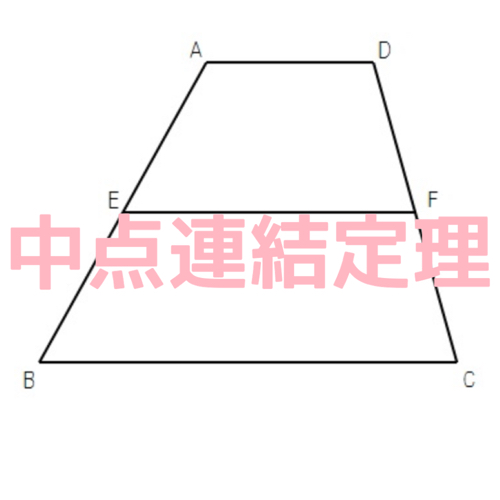


中点連結定理は 相似な三角形についてのお話です さくら塾のブログ
縮尺(縮図 実際の長さが10cmの道は縮尺・・・(2)縮尺5千分の1の地図上で面積が・・・> 相似な図形1 abとcdは平行です。それぞれの図のxの長さを求めなさい。・・・> 相似な図形2 右の図の三角形abcでbcとdeはへいこうです。(1)debcを求めなさい。(2)三角形adeと・・・> 相似な図形3この解き方は「直角三角形の相似」でよく使われます。 基本の考え方だけでも直角三角形の相似の計算はできますが、 こちらの解き方を身につけておくと、 計算速度と正確性をよりアップさせることができます。 a問題3のように、三角形の相似条件 三角形が相似であるためには、次の3つの条件のうち1つでも満たせばOKです。 ①3組の辺の比がすべて等しい abcの各辺をk倍したときにできる三角形を A'B'C'とすると、 A'B'C'の辺は、それぞれ、ka、


円と三角形 相似 中学から数学だいすき



中3数学 相似 直角三角形と相似 Youtube



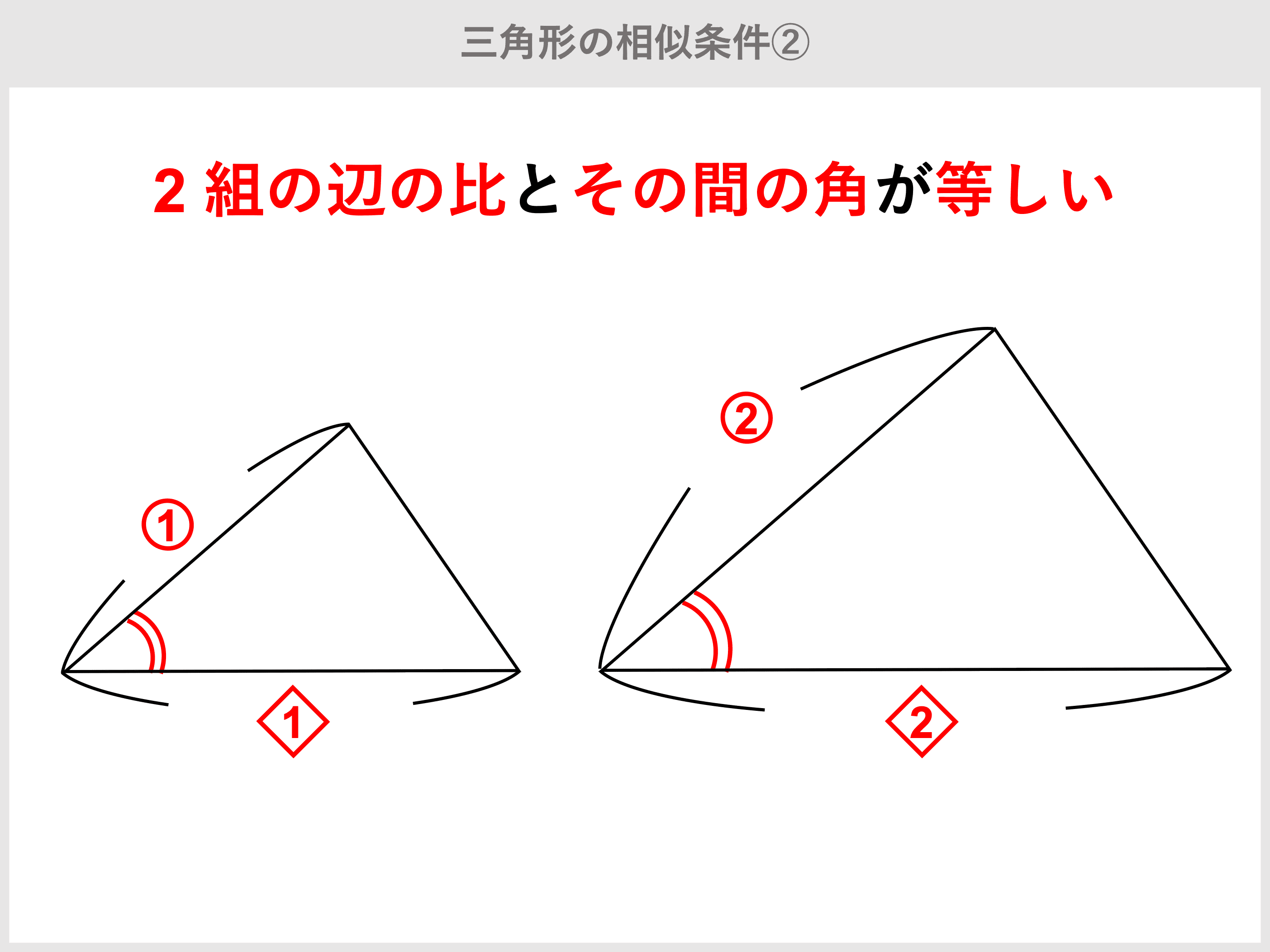
中3数学 三角形の相似条件2 2辺の比とその間の角 練習編 映像授業のtry It トライイット


Studydoctor相似な三角形の辺の比 中3数学 Studydoctor


相似 三角形の相似条件 記号や証明問題も Studyplus スタディプラス


子どもを混乱させる相似な三角形の2つの面積比 算数数学が苦手な子専門のプロ家庭教師みかん先生
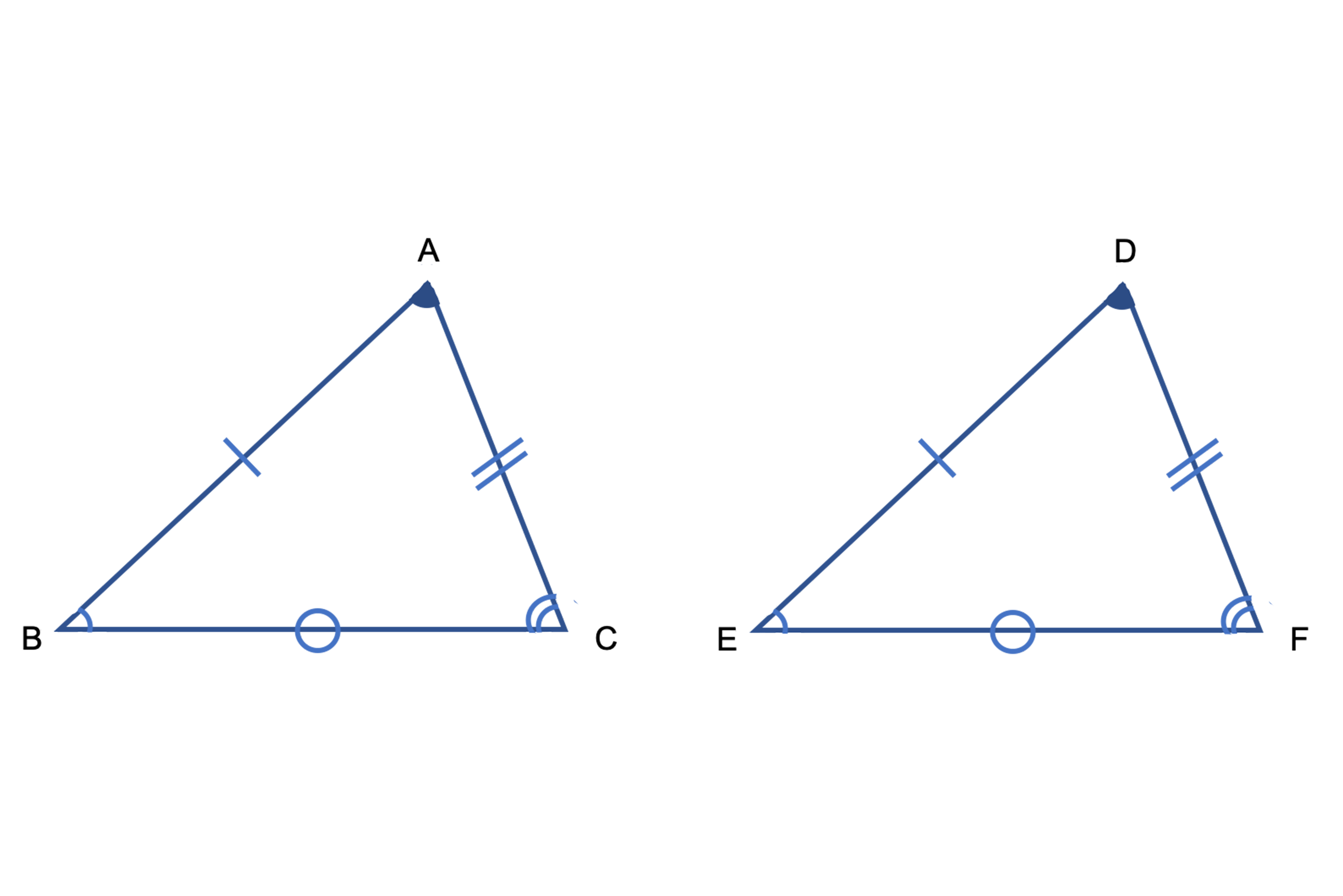


記号にすると と 三角形の 合同 と 相似 の違いをまとめよう 受験に関する豆知識 学習塾ランキング検索総合サイト 塾プラス
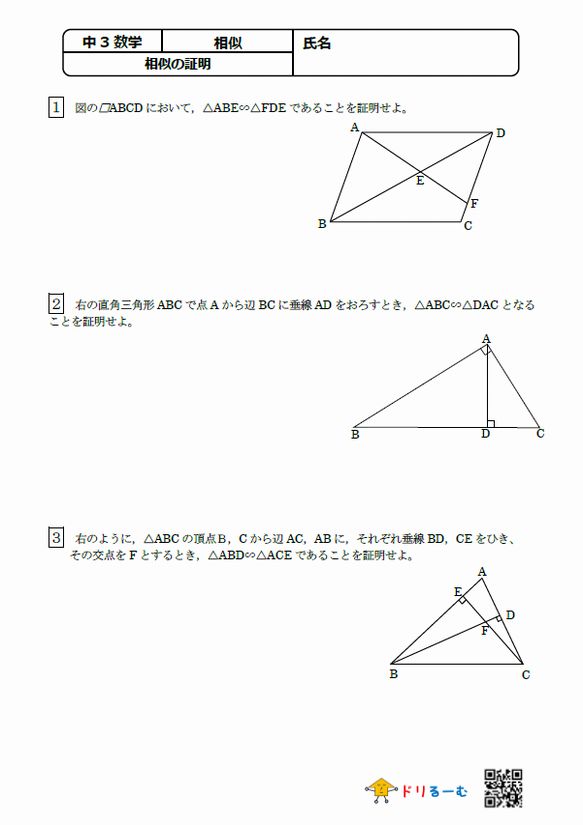


三角形の相似条件 ドリるーむ



中3数学 相似な図形の線分比の定期テスト対策問題 Examee



相似な図形 補助線を引いて考える相似の問題 中学生からの質問 数学 進研ゼミ中学講座 ベネッセコーポレーション



三角形の相似条件と基本的な証明 無料で使える中学学習プリント
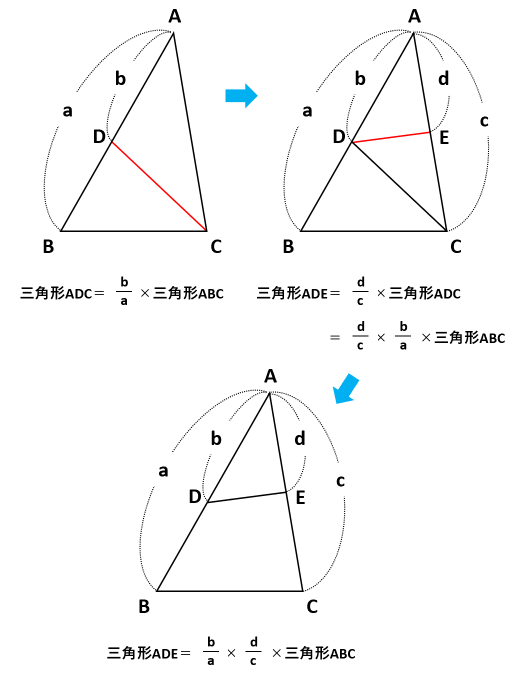


三角形の面積比を求めよう 底辺比と相似比を使えば複雑な問題もスッキリ解決 中学受験ナビ


相似の証明 2つの正三角形と共通な角 勉強ナビゲーター


相似な三角形はどれか 中学から数学だいすき



三角形の相似条件
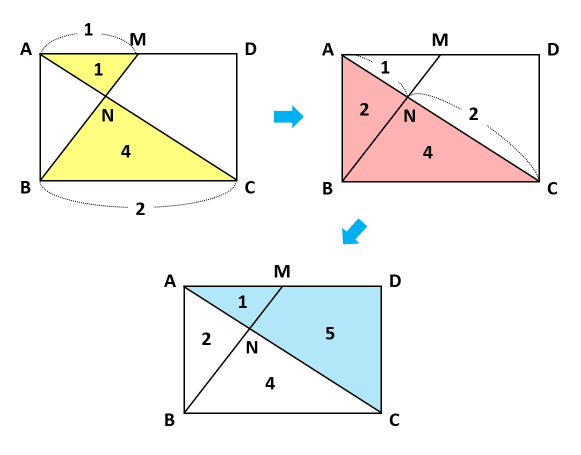


三角形の面積比を求めよう 底辺比と相似比を使えば複雑な問題もスッキリ解決 中学受験ナビ


三角形の相似条件


相似とは 三角形の相似条件 記号 相似比 面積比 証明問題 受験辞典



三角形の相似条件と証明問題の解き方 数学fun


3角形を折る
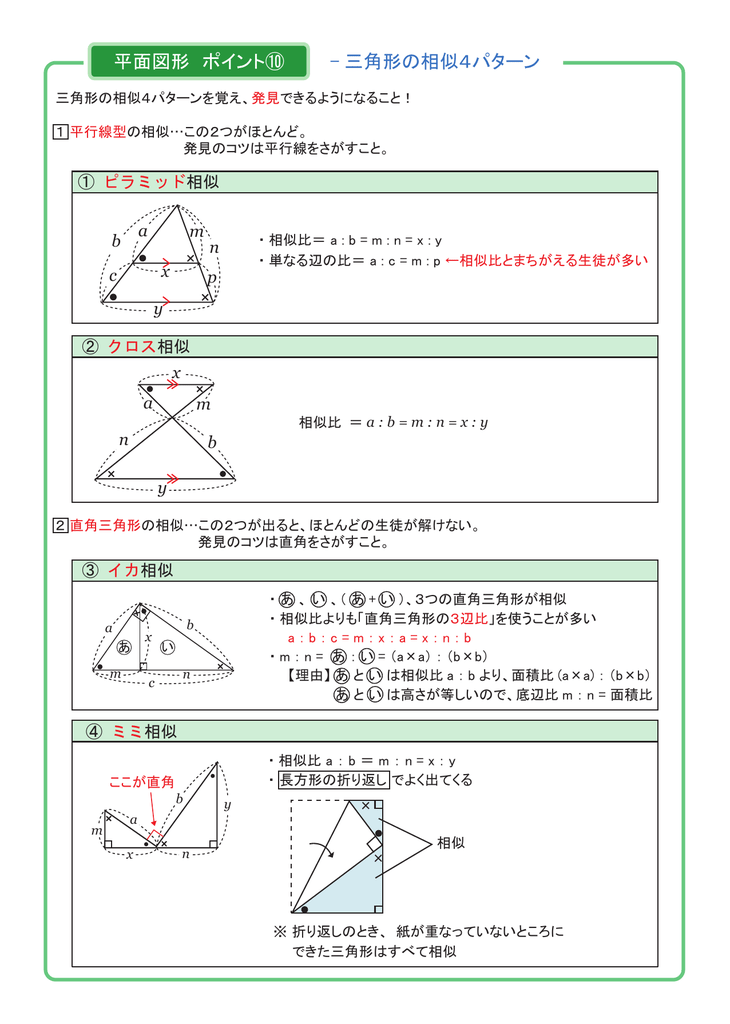


平面図形 ポイント 三角形の相似4パターン
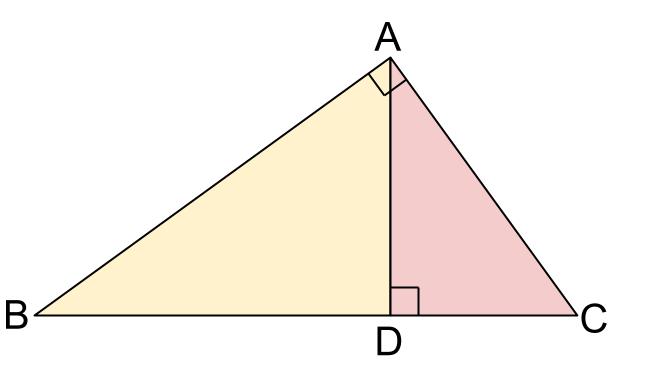


中学数学 直角三角形の相似 中学数学の無料オンライン学習サイトchu Su



相似な三角形を見つける 修正 Youtube


Studydoctor三角形の相似条件 中3数学 Studydoctor



三角形の相似条件が見やすい図で一発理解できる 練習問題付き 高校生向け受験応援メディア 受験のミカタ



三角形の相似に関する質問 勉強質問サイト


相似 三角形の相似条件 記号や証明問題も Studyplus スタディプラス



保存版 三角形の合同条件と相似条件の6つのまとめ Qikeru 学びを楽しくわかりやすく


相似図形



中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ


相似な図形 三角形の相似条件 相似比 勉強ナビゲーター


三角形の相似条件の解説 図形の性質
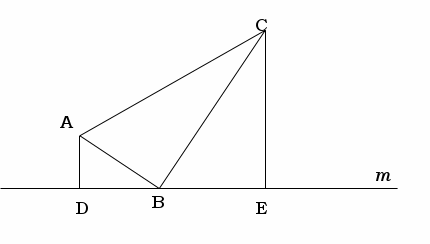


相似の証明2



三角形の相似条件
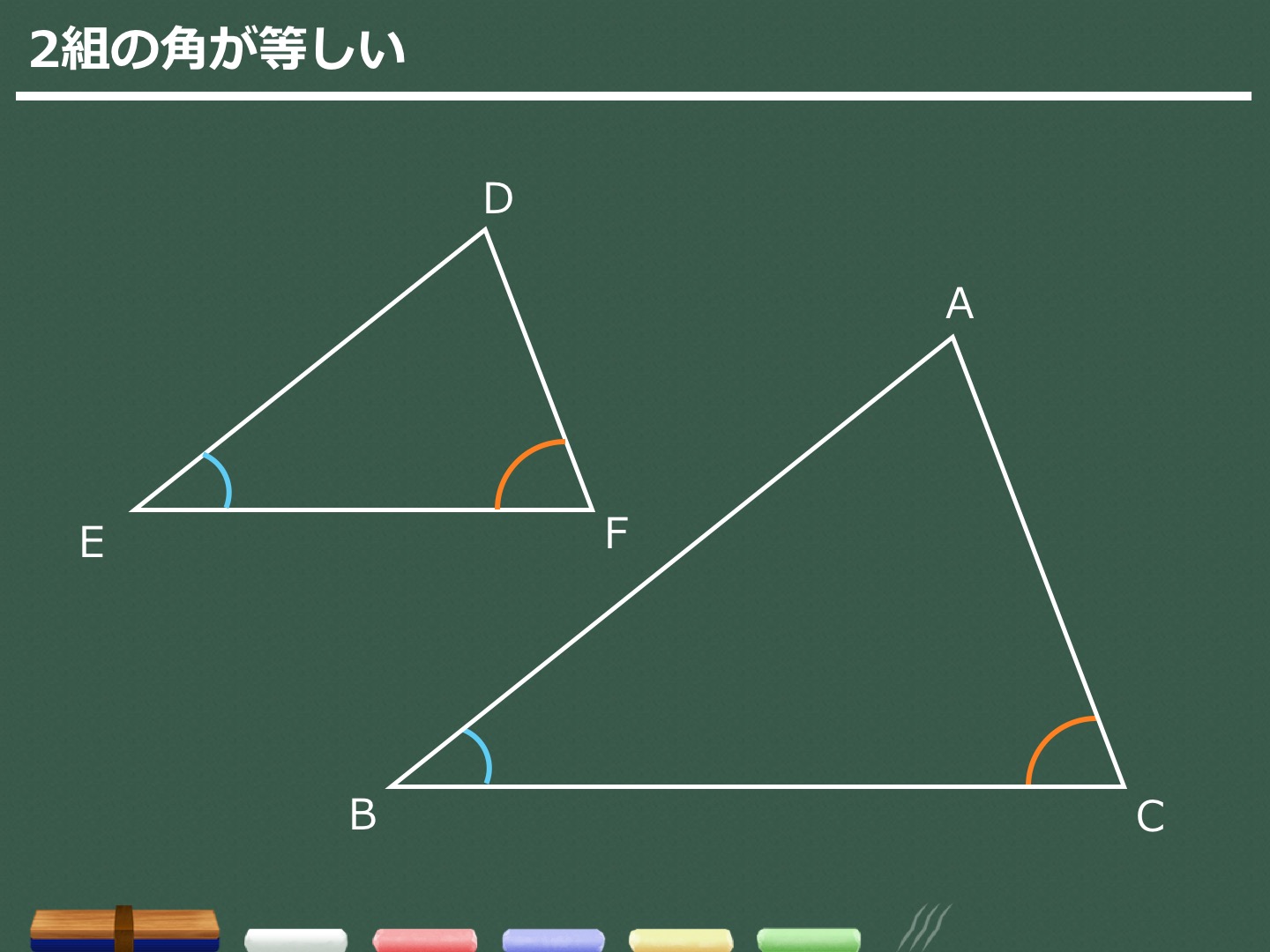


3分でわかる 三角形の相似の性質と条件 証明問題の解き方 合格サプリ
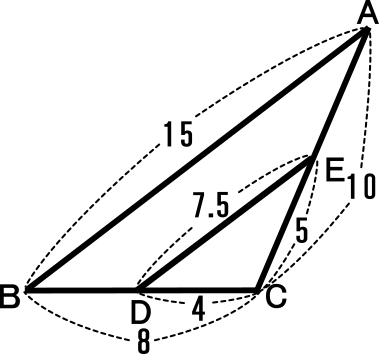


中学3年数学練習問題 三角形の相似条件と証明の問題


相似 三角形の相似条件 記号や証明問題も Studyplus スタディプラス



三角形の相似条件 証明の練習になる簡単な問題を紹介 中学や高校の数学の計算問題
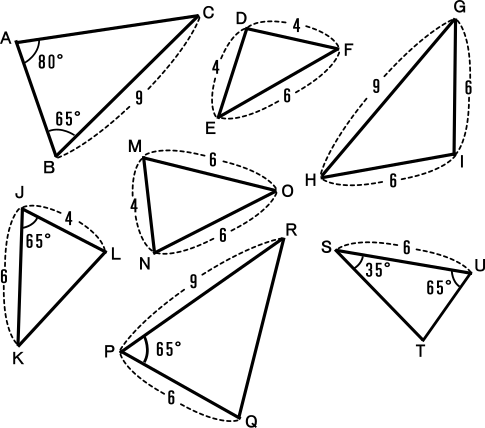


中学3年数学練習問題 三角形の相似条件の問題
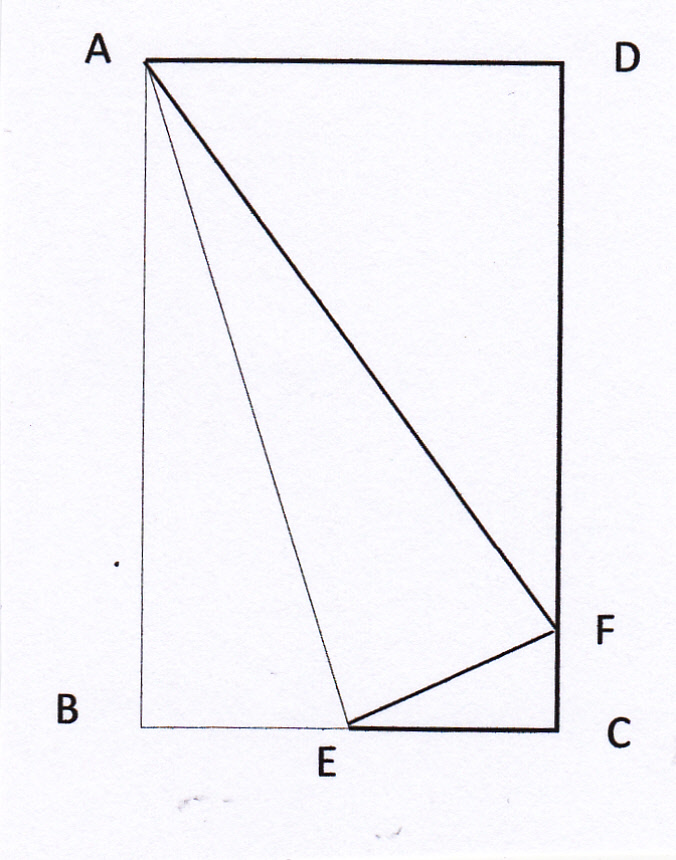


図形の折り返しと三角形の相似の証明 解き方 現役塾講師のわかりやすい中学数学の解き方



三角形の面積比と相似比 チーム エン


Math 相似 直角三角形 正三角形と相似 働きアリ


平面図形の基礎
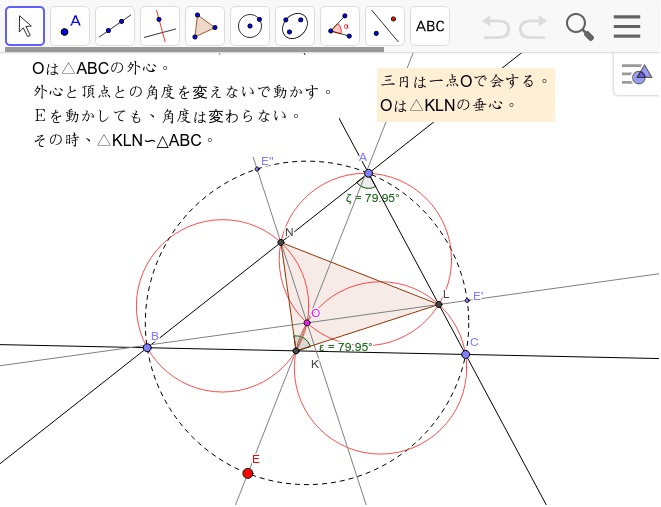


三角形に内接する相似三角形 Geogebra
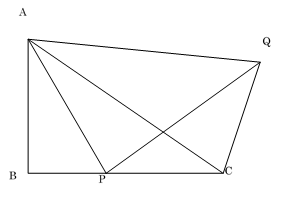


三角形の相似2 中学勉強 おやじさん ネット
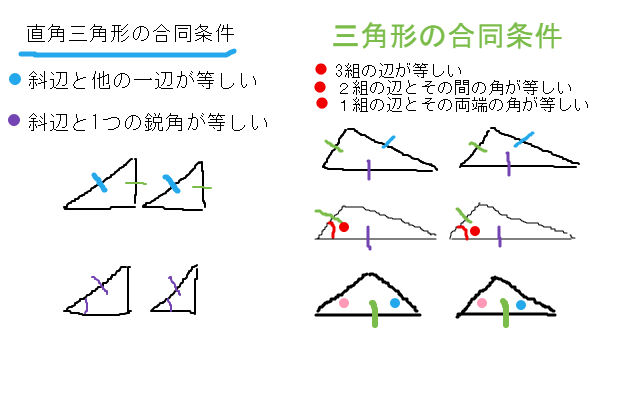


三角形 合同 相似条件 直角三角形の合同条件 中学数学 理科 寺子屋塾の復習サイト



中3数学 三角形の相似条件3 2つの角 例題編 映像授業のtry It トライイット


中学数学 三角形の相似条件 中学数学の無料オンライン学習サイトchu Su


数学 36 の三角比 二等辺三角形を用いて求める方法は 数スタ
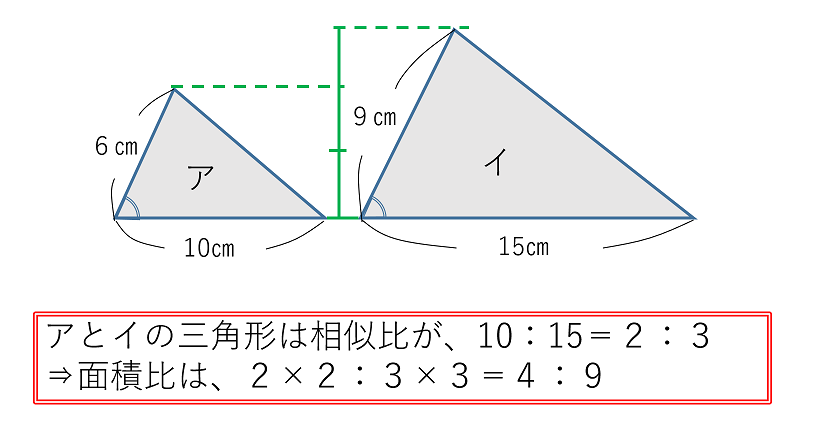


平面図形の苦手を解消 三角形の面積比 基本編 中学受験ナビ
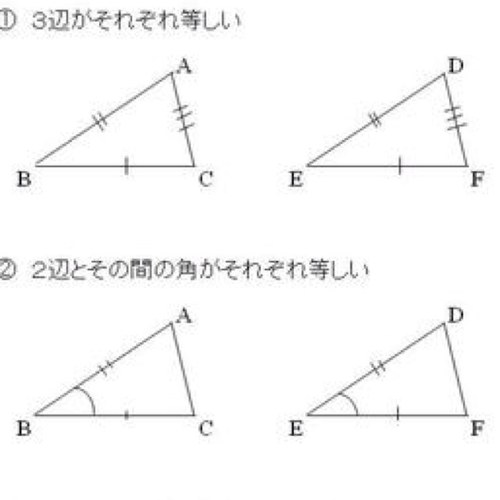


三角形の相似条件bot Triangle Bot Twitter



相似条件とは 三角形の相似条件はなぜ3つなの 証明問題アリ 遊ぶ数学



子供向けぬりえ 最高の三角形 比 定理
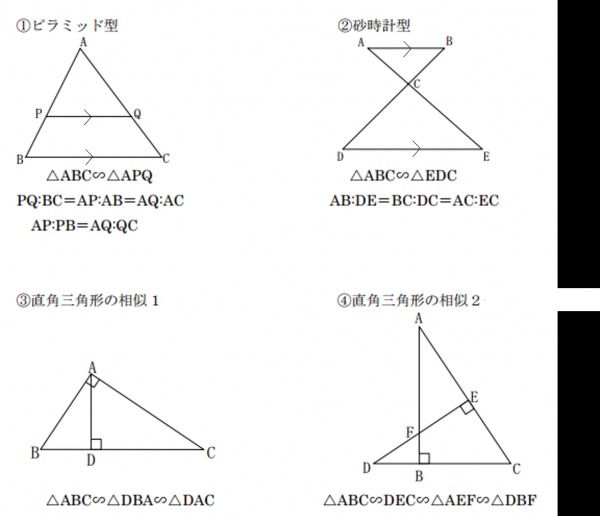


三角形の相似 合同条件 優技録



三平方の定理について考える4 三角形の相似を使った証明方法 身勝手な主張



面積比の公式まとめ 相似比と面積比と体積比の関係もあわせて解説 遊ぶ数学



2つの非相似なヘロン三角形の外周と面積が等しい 円周率近似値の日に生まれて理系じゃないわけないだろ Knifeのblog


中学数学 三角形の相似条件
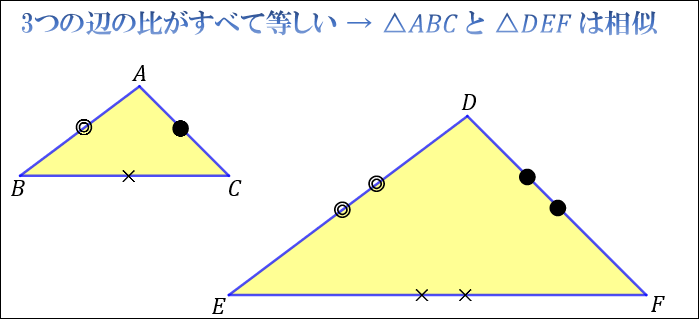


三角形の相似条件について 図解で分かる相似条件 アタリマエ


Studydoctor正三角形と相似の証明 中3数学 Studydoctor
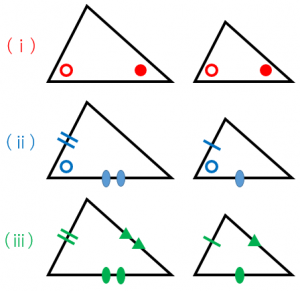


三角形の相似条件と有名な例題3問 具体例で学ぶ数学



5章1節2 三角形の相似条件2 数学のすすめ



三角形の相似条件が見やすい図で一発理解できる 練習問題付き 高校生向け受験応援メディア 受験のミカタ


相似な図形の応用問 右の図のような C 90 の直角三角形があ Yahoo 知恵袋


高校入試数学 相似な三角形の対策問題
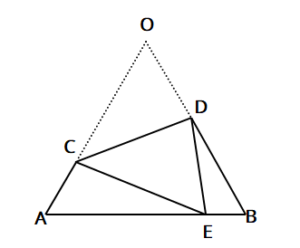


高校入試対策数学 折り返し図形と相似の融合問題 中学生勉強サイトあかね先生
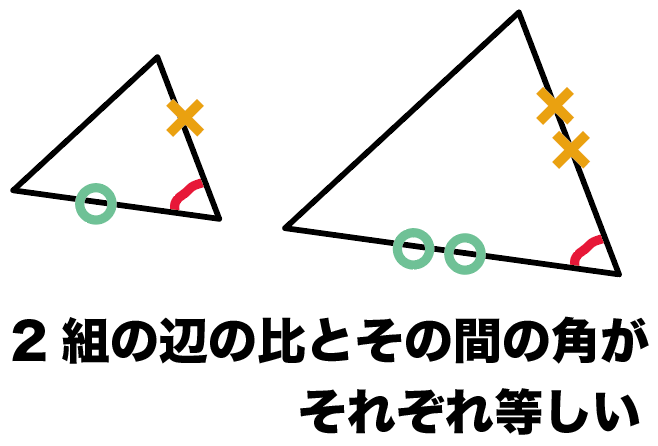


2分でわかる 三角形の3つの相似条件 Qikeru 学びを楽しくわかりやすく
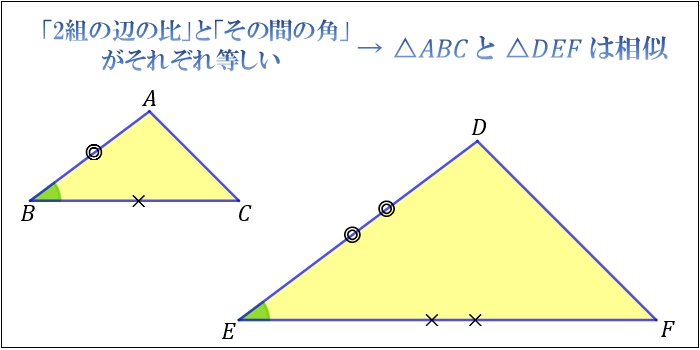


三角形の相似条件について 図解で分かる相似条件 アタリマエ



三角形の相似条件
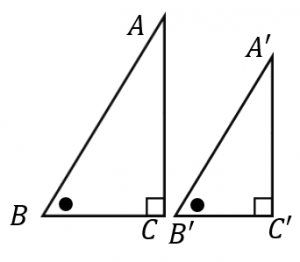


直角三角形の相似条件 具体例で学ぶ数学
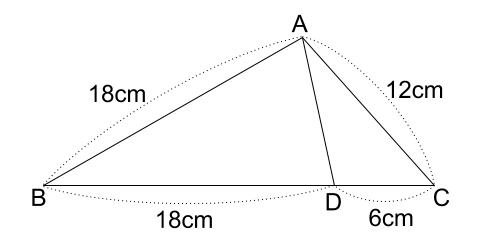


中学数学 相似の証明 その1 中学数学の無料オンライン学習サイトchu Su



中3数学 三角形の相似条件1 3辺の比 映像授業のtry It トライイット
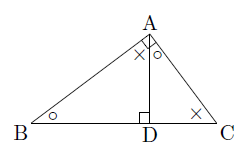


直角三角形と相似 まなびの学園
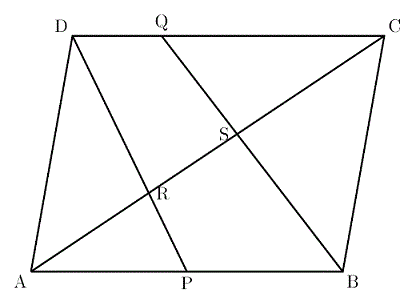


かみのドリル 三角形の相似のドリル 中受
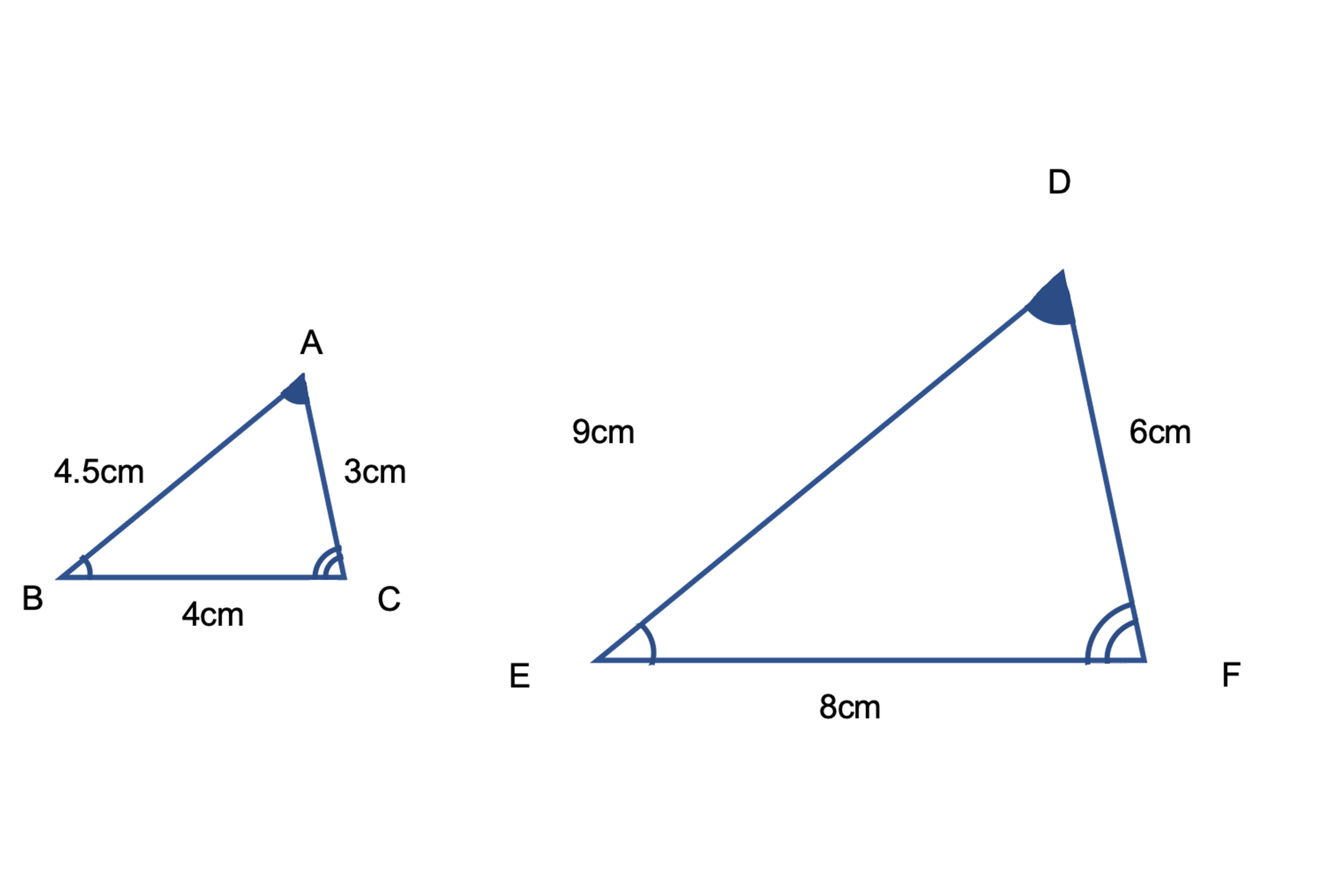


記号にすると と 三角形の 合同 と 相似 の違いをまとめよう 受験に関する豆知識 学習塾ランキング検索総合サイト 塾プラス



相似な図形の面積比の問題 相似比を出してから二乗しよう 中学や高校の数学の計算問題
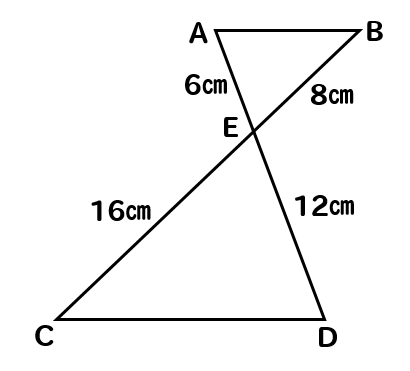


中3数学 相似な図形の見つけ方 相似条件とは 基本問題を使って解説 数スタ


Math 相似 直角三角形 正三角形と相似 働きアリ
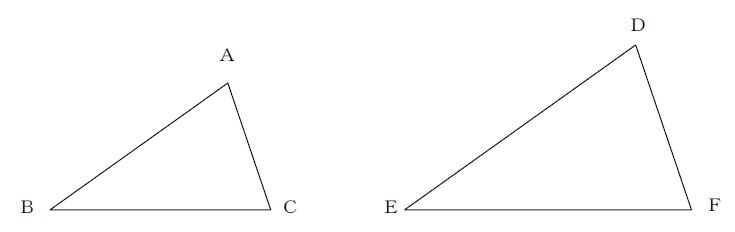


中3数学 相似な図形と相似条件のポイントまとめ やすひこ先生の中学生授業log
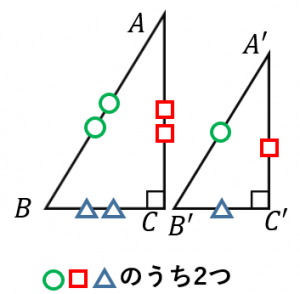


直角三角形の相似条件 具体例で学ぶ数学
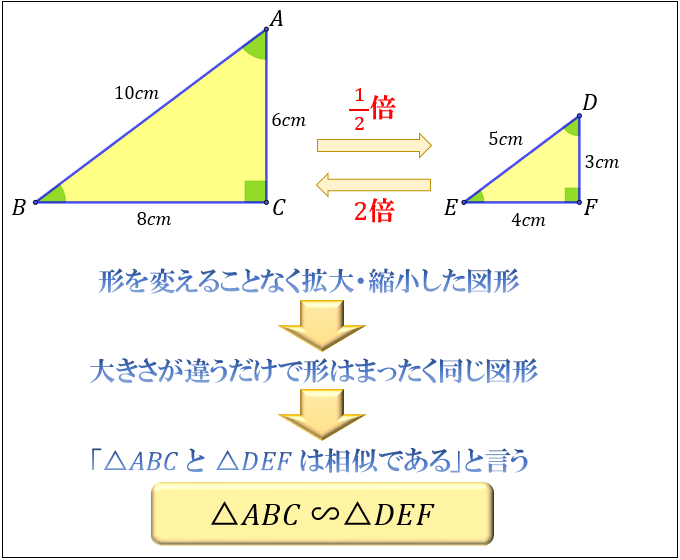


相似とは何か その意味 合同との違い 相似な図形が持つ性質について アタリマエ
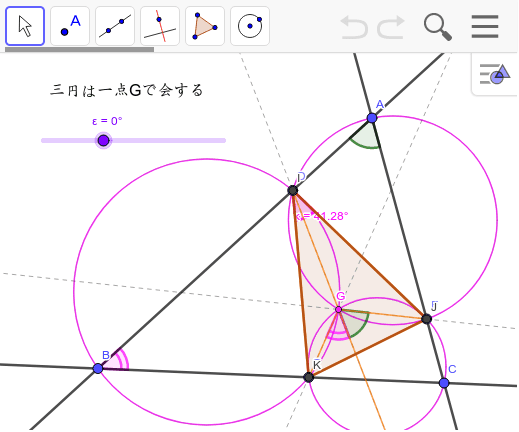


三角形に内接する相似三角形 Geogebra
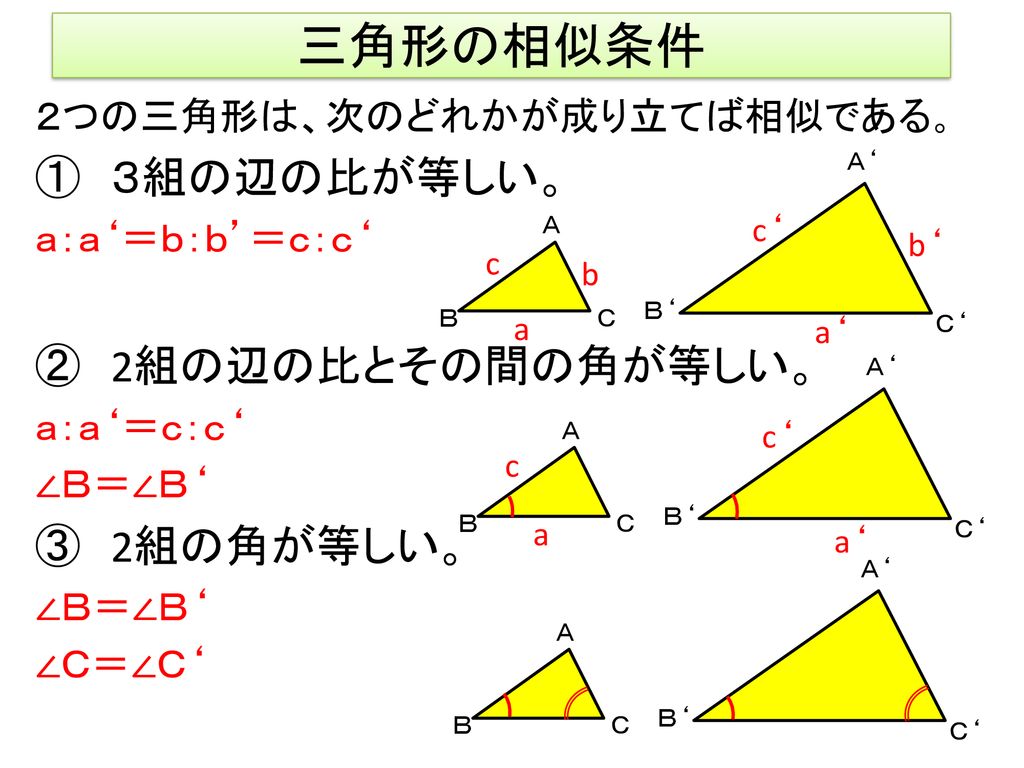


本時のねらい 図形の中から相似な三角形を見出し 相似条件を用いて証明することができる Ppt Download



相似な図形 三角形の相似条件 中学数学 By となりがトトロ マナペディア
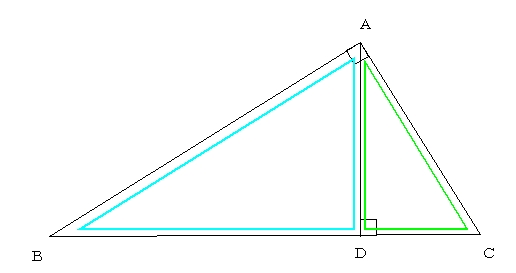


相似 直角三角形
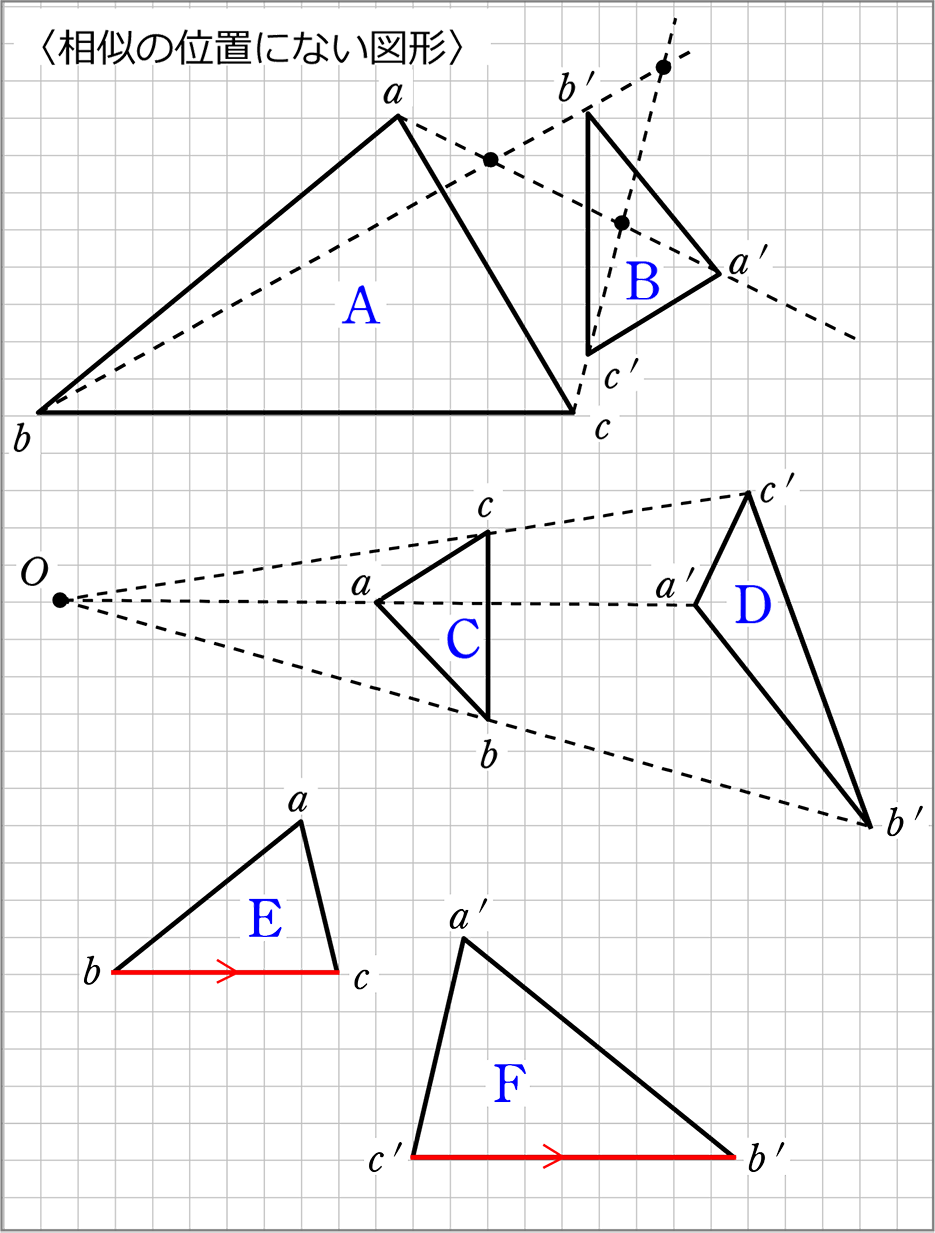


中学数学 図形の相似


中学数学 三角形の相似条件
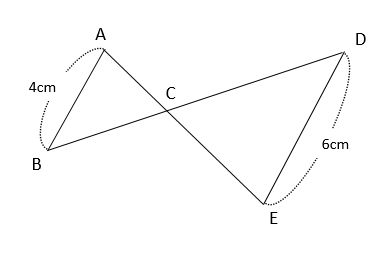


相似 平行線と三角形の問題ではちょうちょかピラミッドを探せ みみずく戦略室
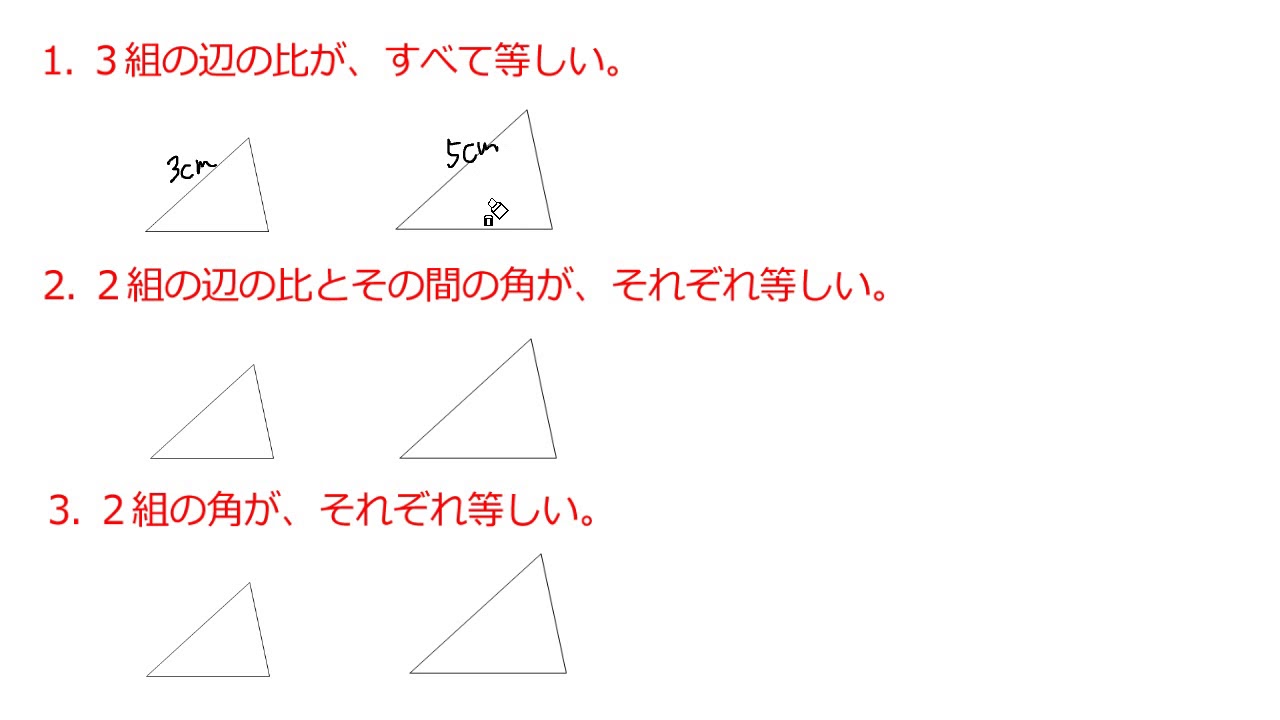


三角形の相似条件 修正 Youtube
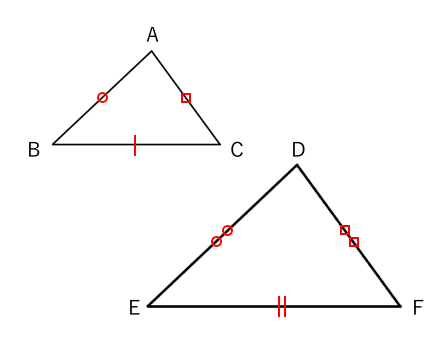


相似な三角形 相似条件とは 苦手な数学を簡単に
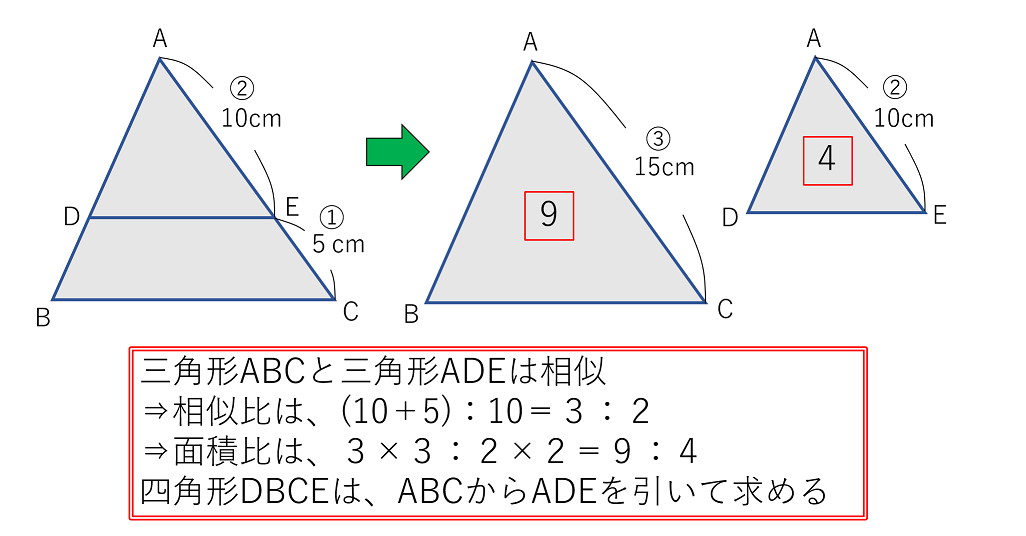


平面図形の苦手を解消 三角形の面積比 基本編 中学受験ナビ
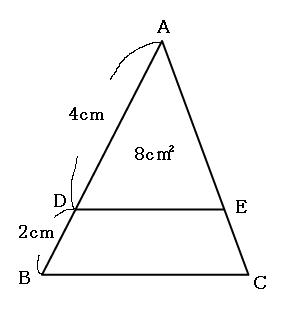


相似比と面積比と体積比の関係の公式を使って面積や体積を求めよう
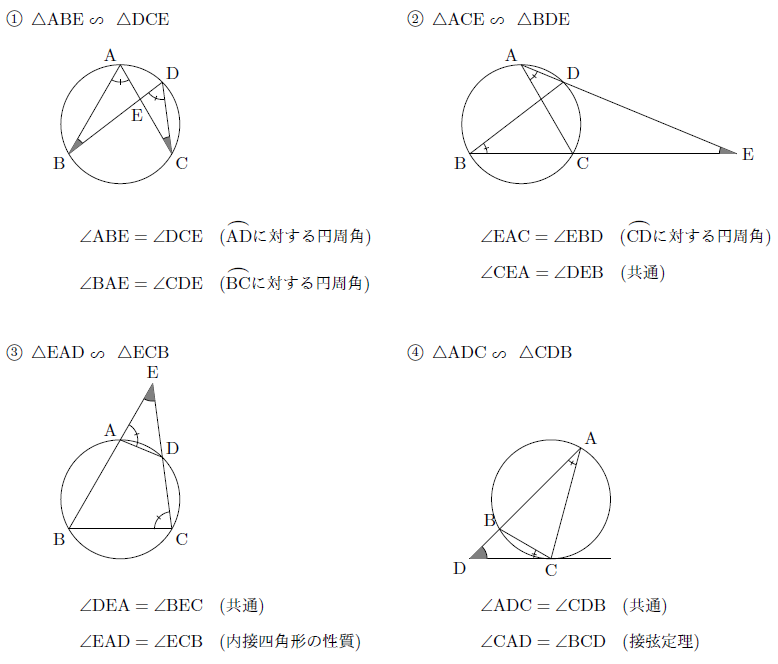


円と相似 まなびの学園



三角形の相似条件が見やすい図で一発理解できる 練習問題付き 高校生向け受験応援メディア 受験のミカタ


2つの正三角形と相似



0 件のコメント:
コメントを投稿