32 電磁波の正準方程式 (まだ古典電磁気学) 電磁波の方程式をハミルトンの運動方程式 P˙ =− ∂H ∂Q, Q˙ = ∂H ∂P (324) の形に書き直す。このような形式を得られれば、正準量子化が可能になる。以下、 • まず周期的境界条件の下で、A(r,t)を基準振動で展開 異なる媒質間での境界条件 屈折率の異なる媒質の境界で, 光線は反射や屈折を起こす 入射した光のエネルギーのうち, どれだけが反射して, どれだけが透過するのかは, 電場成分や磁場成分の境界条件を考えるだけで計算できてしまうのである その境界条件というのはマクスウェル方程式から導かれるのだが, 結論から言えばとても簡単である ・境界面に point 波(電磁波・音波)が,異なる媒質の境界面に対し垂直に入射した場合の反射・透過について. 量子力学で,1次元の階段型ポテンシャルに平面波が入射したときの反射・透過について. これらの波動現象が,ほとんど同じ方法で扱えることを,計算を比較しながら確認する.

金字塔能量之迷 五 每日头条
電磁波 境界 条件
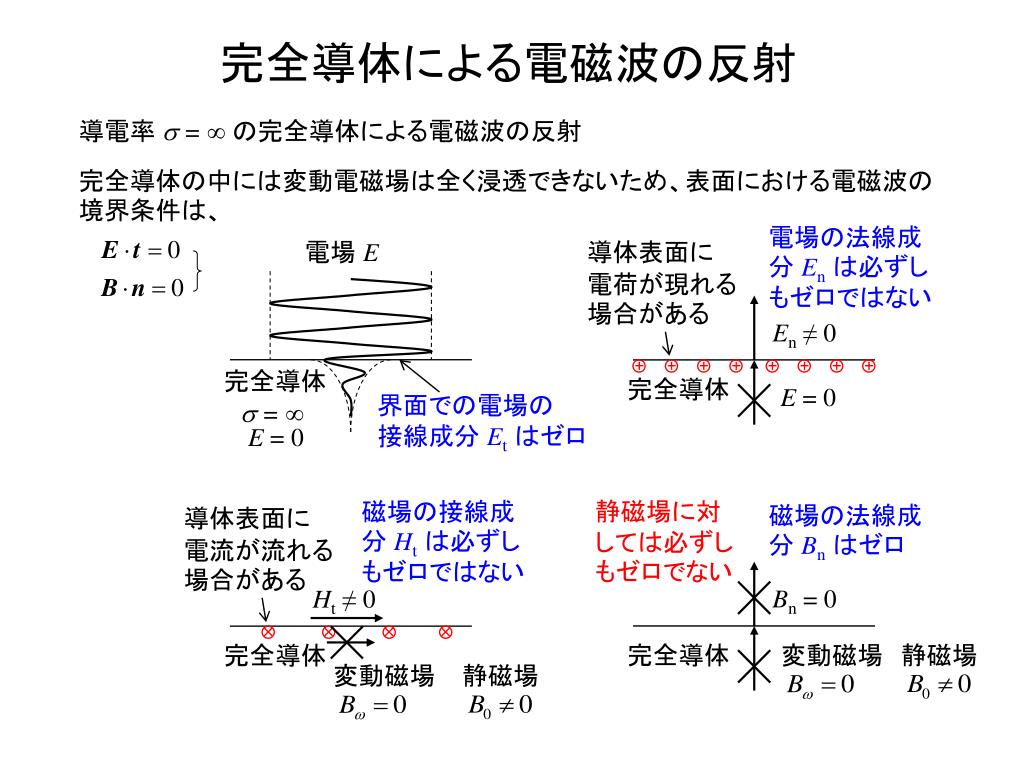
電磁波 境界 条件-求める境界条件は、 と E t =0 H n =0 (B n =0)である。 2 完全導体に入射する電磁波の電界を iy = 0 −ωE E i kx t LL exp ( ) (5) (ω=2πν)とすると、磁界はz 方向に振動しており 0) 0 0 H E t iz ω μ ε = Ery = 0 t) exp (i kx − Ery で与えられる。 一方、完全導体で反射された反射波の電界 は、導体表面平面波と境界条件 1 1st Lst v26 Jan21 電磁波における境界条件の使途 Region 1 Region 2 透過 (未知) 111 111 H jE E jH 222 222 H jE E jH 22 EkE1110 22 EkE21 11 1




網友激推防電磁波布熱銷排行 松果購物
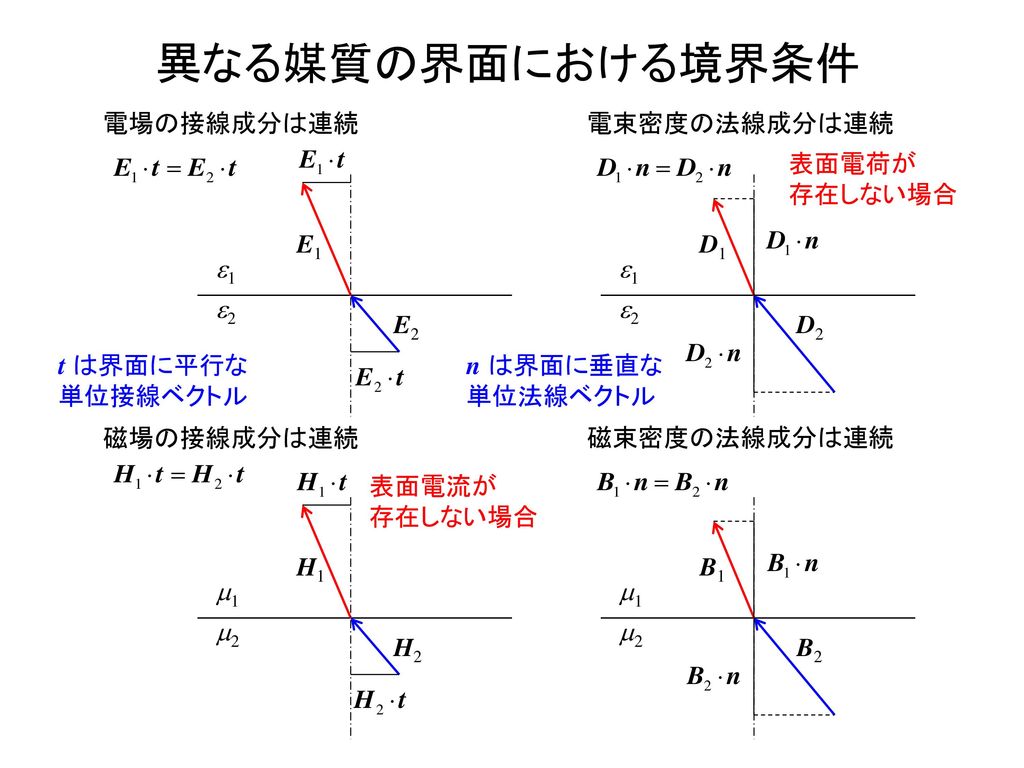
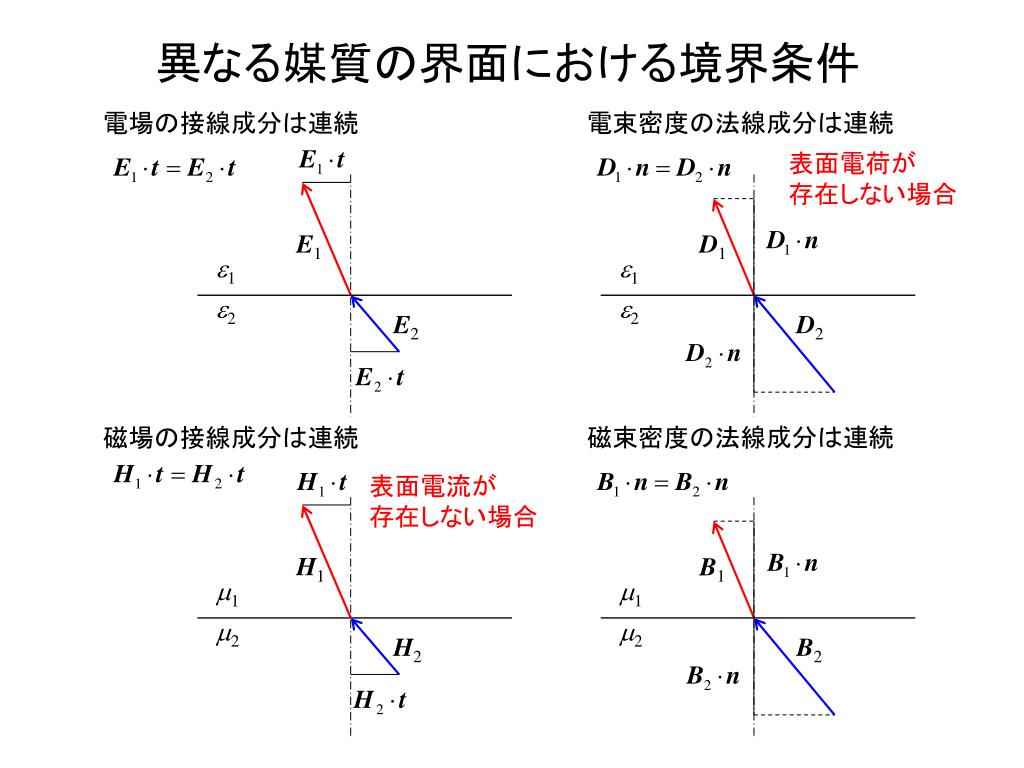
H2 DS C 異なる媒質の界面における境界条件 E1 E2 e1 e2 電場の接線成分は連続 H1 H2 m1 m2 磁場の接線成分は連続 電束密度の法線成分は連続 D1 D2 e1 e2 磁束密度の法線成分は連続 B1 B2 m1 m2 表面電荷が 存在しない場合 表面電流が 存在しない場合 t は界面に平行な単位接線ベクトル n は界面に垂直な単位法線ベクトル 界面での反射と透過 2種類の媒質が xy 平面 (z = 0) を境に接し境界条件 rot t ∂ =− ∂ B E rot t ∂ = ∂ D HJ divB =0 divD =ρ 電磁界に関するすべて の性質はMaxwellの方 程式に記述されている。電磁場の異なる物質面における境界条件 物質中のマクスウェル方程式は、形式的には e0 e, m0 m として得られるが、 D (= e E), H (=B/m) と E, B の使い分けに注意する必要がある。 また、物質中の光速度は、 v = w/k = 1/√em である。 境界条件1: E の接線成分が連続
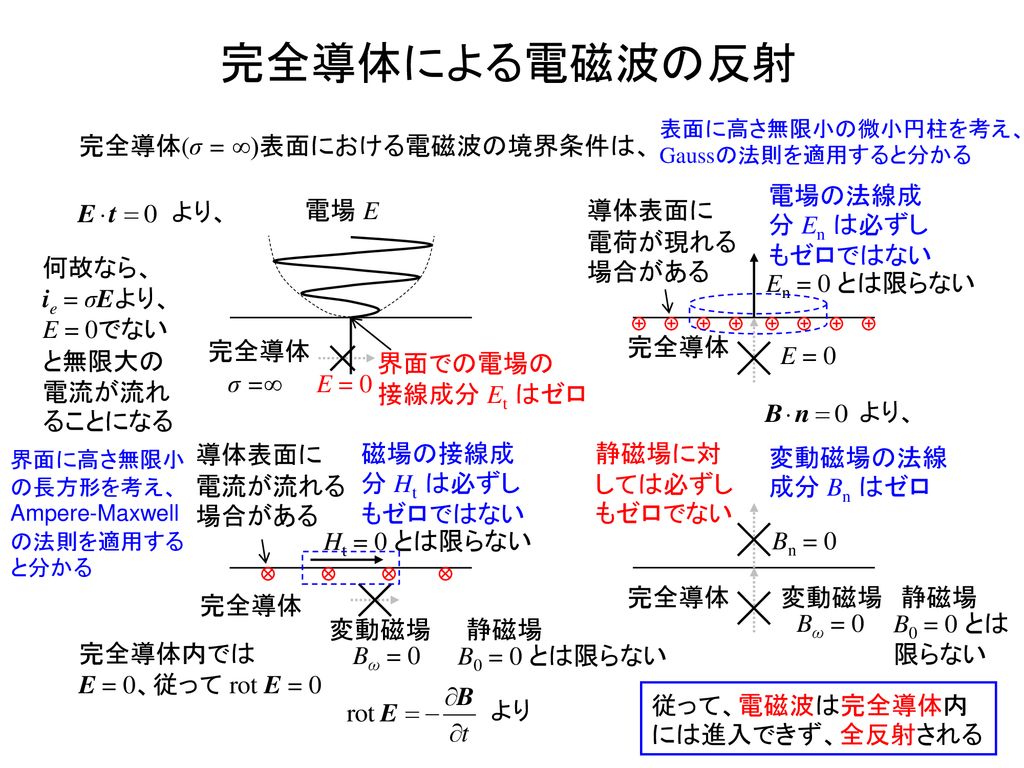
電磁波伝搬を解析するときに、銅などの良導体を完全導体壁とすべきか、表面インピーダンス近似した境界条件を使用すべきかが気になった。 よって、完全導体壁と表面 インピーダンス 法を Maxwell 方程式から導出して、その違いを検討したい。図2 電束密度の法線成分に対する境界条件の計算 導体中電場が存在しない→ 電束密度も存在しな い:領域1を真空、領域2を導体(図2(b)) σn = Dn = ε0En (15) 静電誘導:外部からの電場による導体の表面電荷 の誘起 12 表皮効果 導体中の変動電磁場(図3) rot吸収境界条件 吸収境界条件(ABC, Absorbing Boundary Condition) :FEM, FDTDは このように全空間にメッシュを切るた め、開放空間を模擬する。 物体からABCまでの距離:1/2波 長以上 ABCは垂直入射平面波をうまく吸 収するように出来ているので、なるべ く離した方が良い。
電磁気学III 第4講 5 E (419)0 ここでE x0は境界条件で決まる定数である。E x0は一般に複素数である。 初期条件としてE x = 0, E y ≠ 0とすれば、以下のようなEが常にy成分しかもたない解となる であろう。 (4) ここでE y0は境界条件で決まる定数で、一般に複素数である。境界条件 絶縁体と絶縁体の境界面をまたぐ高さδの長方形cを考えると,閉曲線cに沿って 電場(磁場)を一周積分したものはcを貫く磁束(電束)の時間的変化率に等しいが,δ→0の 極限では0となる。電磁波のふるまいを理解するうえで参考となる分布定数線路を表す伝送線路方程式を導出する. 固有伝搬定数,固有インピーダンス・境界条件 電磁波を取り扱ううえでの基本パラメータである固有伝搬定数,固有インピーダンスを求める.



2



Http Www Wsbookshow Com Uploads Bookfile 1612 1 Pdf
キーワード電磁波,散 乱,ス トリップ導体,端 点条件,点 整合法 1 ま え が き ストリップ導体による電磁波の散乱問題は,二 次元 境界値問題の基本的な問題として興味深いばかりでな く,有 限および無限個のストリップ導体の散乱問題を平面波の入射方向が上と異なるときは、電磁界が周期的になりませんので、 周期境界条件を使うことはできません。 なお、周期境界条件がx方向またはz方向のときも同様です。 eemfdmはx,y,z軸に関して対等に扱います。以上の議論は一般の電磁場 (E=∇φdA/dt) に対しては成り立たないが、 TEM 波の場合は進行方向と垂直な電場に対して E = ∇φ が成り立つから TEM 波の方程式は静電場と同じになる。一方、境界条件 φ(導体表面) = 一定



Http Sirius Imass Nagoya U Ac Jp Saitoh Em3 E9 9b E7 A3 81 E6 B0 97 E5 Ad A6iii Ef E7 Ac Ac7 E8 Ac 9b Ef Pdf
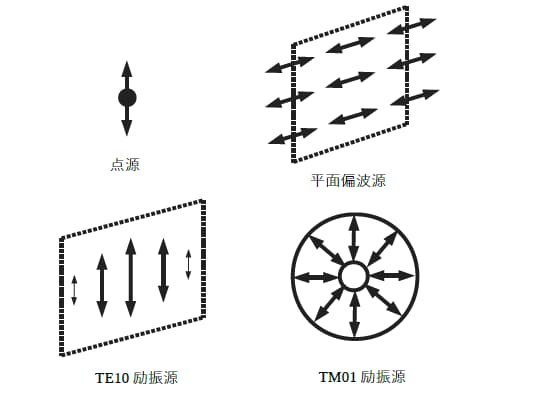



励振源 境界条件 収束判定 解析の実効値 株式会社科学技術研究所
その際のポイントは ①境界条件 と ②電磁波の横波条件 です。Bの垂直成分が連続となる(Maxwellの境界条件)。ここで、 は入射、反射、透過波の波数ベクトルの単位ベクトル、である。 入射波 屈折波 反射波 Maxwellの境界条件( )は境界面に垂直な単位ベクトルとする。 ① ② ③ ④ (a) は常にと垂直(S偏光) ① は自動波面の曲率 エルミート・ガウシアンビーム 分極と電場の関係 (誘電体)薄膜導波路 入射角の条件と開口数(NA) TE波とTM波 固有モードの条件 復習:TE波の全反射 スライド 79 可能なsinq の値 固有モードの波数ベクトル モードの数 固有モード(TE波)の空間パターン 二次元導波路 導波路内の群




電場の数値解析 有限差分法 Fdm 基礎編 Qiita
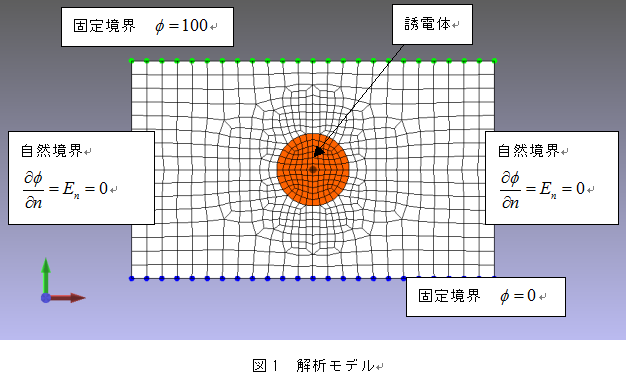



その12 電磁場の境界条件について 株式会社フォトン
Minoru TANAKA (Osaka Univ) 25 誘電体の境界条件 • 2種類の誘電体,誘電体1と誘電体2,の境界面を考える.それ ぞれの誘電率をε1,ε2 とし,境界面に電荷はないものとする. 境界面を囲む微小なうすい円筒(底面積 ΔS) を考えて,ガウスの法則を適用すると, (1) D(r)dS =05 電磁波の反射・透過・散乱 51 電磁界の境界条件 2つの異なる媒質の境界面においても電磁界はMaxwell の方程式で規定される物理的な条件を満足しなけ ればならない。これが電磁界の境界条件である。2種類の媒質が境界面で接するとき,それぞれの媒質中での 媒質定数をそれぞれ添え字1, 2 で表現すれば境界条件は次式で与えられる。) nH H J×− =() 12 S (511) ) nEE×− =()0電磁界の境界条件により,境界面(y = 0)に対する電界と磁界の接線成分は連続でな ければならない.この場合,接線成分はと成分になるので E i z E r z = E t z , H i x H r x = H t x (15) したがって, e– j k 1 xx R h e – j k x = T h e – j k2 x (16) h – cos θѳ 1 η 1 e– j




逆l形アンテナ アース理論実証 その13 誘電体 6 電磁波の 電界と磁界の境界条件の関連性 Jo3krpの独り言



完全導体境界条件 Ykondo813 S Diary 旧パワエレ Emc日記
この方程式でマクロな電磁気、電磁波現象の全てが記述可能 (媒質条件、励振条件、境界条件は与える) 2998 10 / sec c 1 u 8 m PH ①波になる ②速度は光速と一致 解いてみると 「電磁波」と名付けた 光は電磁波の一部と考えられる アンペアの法則は無限長電流電磁波 (時間依存): (ewt) または(temw)を右クリック>散乱境界条件を選択し、外部領域との境界を選択します。平面波の垂直入射 1 1st Lst v34 May21 電磁波における境界条件の使途 Region(1) Region(2) 透過 (未知) 111 111 H jE E jH ωε ωμ ∇× = ∇× =− 222 222 H jE E jH




Woa1 電磁波吸収構造体 Google Patents



初中生看阅兵要看本质阅兵式的中考考点大汇整 组图
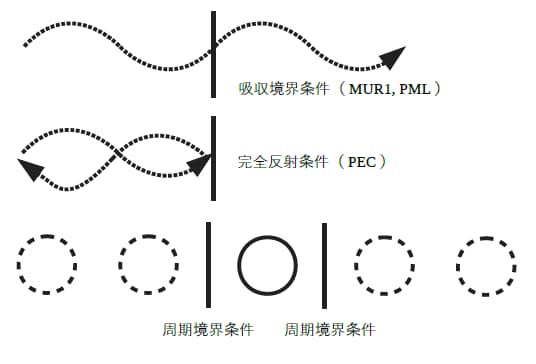
境界条件 3種類の境界条件 電磁波シミュレーションで用いられる境界条件は主に上に示した3種類です。 MUR1及びPML (Perfect Matched Layer)は電磁波の反射を0にする条件として定式化されているため吸収境界条件と呼ばれますが実際には解放をモデル化する場合に使用されます。 完全反射条件PEC(Perfect Electric Conductor)は入射した電磁波を完全反射する条件です。 導波管やを進める.まず,電磁波がある角度で1つの境界面へ入射 する場合を考える(図2).ここでは,境界面を 面にとっ ているので,電磁波の入射面を 面にとる.入射波 ,反 射波 ,透過波 の各成分に対する境界条件は,式(3), (4)で与えられ, (12) (13) となる.アンペールの法則(式(2))の 成分と式(12)から, (14) は『電磁気学第2』講義資料No2 電磁波の発生 電荷分布や電流密度を与えると、マックスウエル方程式を解くことにより電磁場を求めることができる。 そして、それらが時間変動すると電磁波が発生する。 1 遅延ポテンシャル




05 号 電磁界解析装置 電磁界解析方法および電磁界解析プログラム Astamuse




金字塔能量之迷 五 每日头条
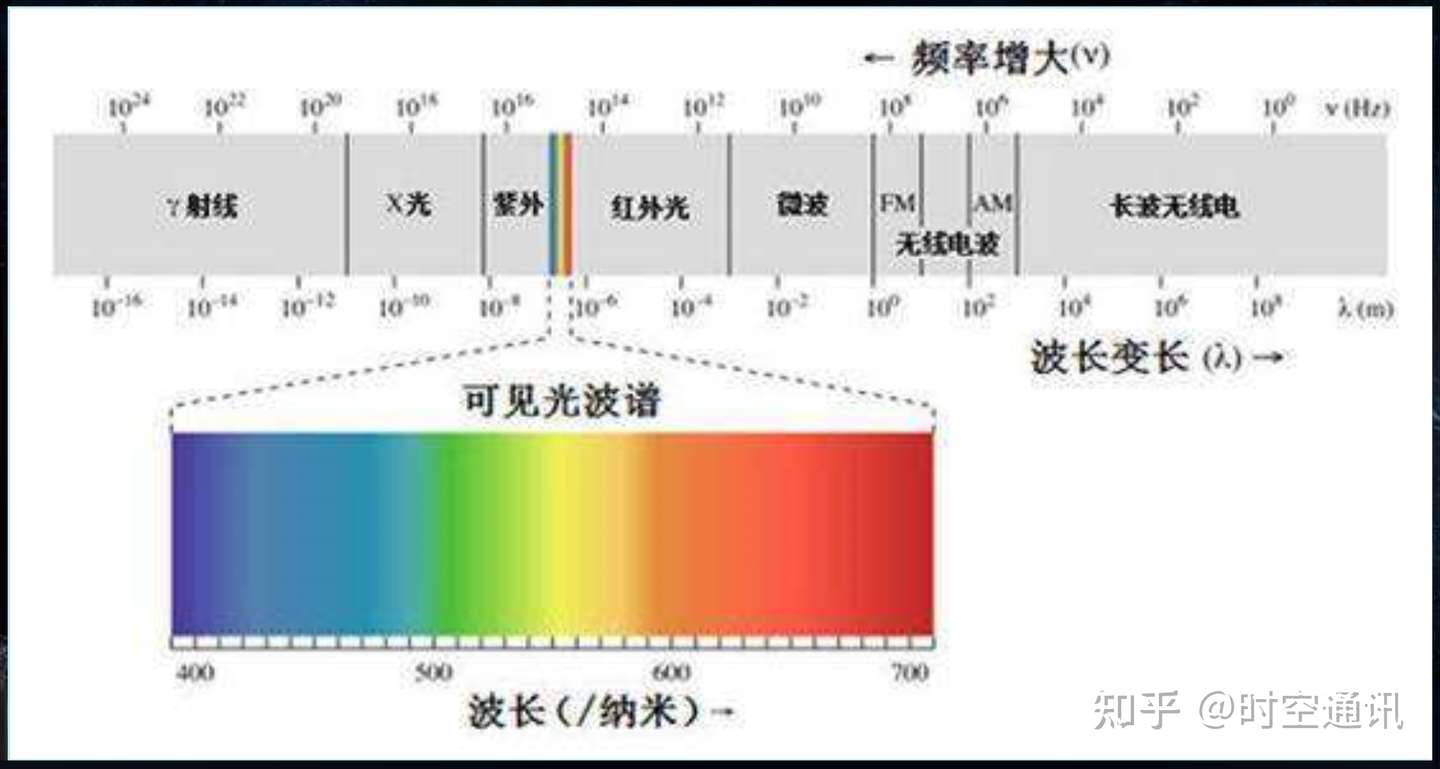
境界条件の種類 電磁波解析で使える境界条件は8種類あります。 • 電気壁 • 開放境界 • 磁気壁 • 表面インピーダンス項目 条件 ソルバ 電磁波解析Hertz熱伝導解析Watt解析の種類 電磁波解析:調和解析 熱伝導解析:定常解析 解析オプション 面(辺)電極の厚みの影響を無視するをチェック※電磁波(でんじは 英 electromagnetic wave)は、電場と磁場の変化を伝搬する波(波動)である。電磁波は波と粒子の性質を併せ持ち、散乱や屈折、反射、また回折や干渉など、波長によって様々な波としての性質を示す一方で、微視的には粒子として個数を数えることができる。電磁波の量子は光子である。電磁放射(英 electromagnetic radiation)とも呼ばれる




电磁场 哈尔滨工业大学 中国大学mooc 慕课



電磁波の完全導体の境界条件についての質問です 境界面で Yahoo 知恵袋
POINT 散乱問題と同じように,「定常的な状態を扱う方法」と「波を追跡する方法」がある. 前者では「定常的な解+境界条件」をもとに解き,後者は「すべての反射波・透過波(この際,境界条件を考慮)を合成する」ことで解く. 関連記事 層・垂直入射の反射と透過(電磁波弾性波および電磁波動場における吸収境界条件とその特性 密度・誘電率を複素数にしての数値計算 An Absorbing Boundary Condition with Complex Density and Dielectric Constant for the Calculation of the Elastic and Electromagnetic Wave Fields




網友激推防電磁波布熱銷排行 松果購物



买多优选医之本吸地气少生病理疗鞋的原理是什么 价格多少钱 大湖在线



9章 反射と屈折の法則




スライドインタフェースを用いた導波管の電磁波解析 株式会社フォトン



改运就是扬升频率 意识




Pdf 卫星遥感影像处理技术分析




電磁波 時間依存 インターフェースにおいて線電流を印加したい 計測と制御とcaeソフトウェアの計測エンジニアリングシステム株式会社




风水太极场




電場磁場電磁波 投書 高壓電塔真的會致癌嗎 為 電磁波 闢謠 Ddmba




境界条件 ムラタソフトウェアブログ
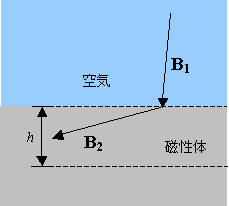



電磁気学における磁性体の境界条件1




03 0726号 電磁波透過構造体の評価方法 Astamuse



Research Kosen K Go Jp Researcher List Read Pdf



Http Www Kusamalab Org Lecture Em2 D6 Plane Wave Slide Pdf



买多优选医之本吸地气少生病理疗鞋的原理是什么 价格多少钱 大湖在线



Http Psroc Org Tw Bimonth Images Uploafiles Files E7 E7 90 86 E9 9b 99 E6 9c E5 8a28 2 401 518 Pdf




金字塔能量之迷 五 每日头条



Www Muratasoftware Com Support Download Files Seminar Femtet Hertz 1 Pdf




逆l形アンテナ アース理論実証 その12 誘電体 5 磁界の強さhの境界条件 Jo3krpの独り言




高等学校教材 工程电磁场与电磁波 摘要书评试读 京东图书



灯光和太阳光能量完全不同 亮度也相差巨大 速度会不同吗 知乎



アクティビティ 通信工学研究室




水和空气均无色透明 为何我们能够看见水 却看不见空气 网易订阅
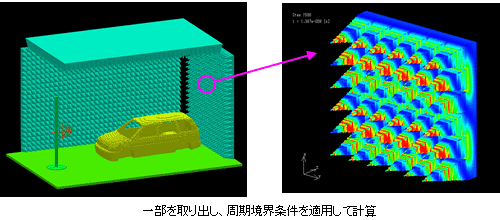



Magna Tdm 特徴 周期構造物に対して周期境界条件の適用が可能



2




上海迎华电子科技有限公司



解析シミュレーションソフトfemtet のバージョンアップと第24回設計 製造ソリューション展への出展について 村田製作所 Aeg 自動車技術者のための情報サイト Automotive Engineers Guide



異なる媒質の境界における電磁波と電子波 2 1 異なる媒質の境界における波動の一般論




綺麗な電磁波 解析 最高の花の画像



Emc与emi技术与器件资讯 电子发烧友网



风水太极场



電磁気学 Electromagnetics 6 5講義分 電磁波の反射と透過 山田 博仁 Ppt Download
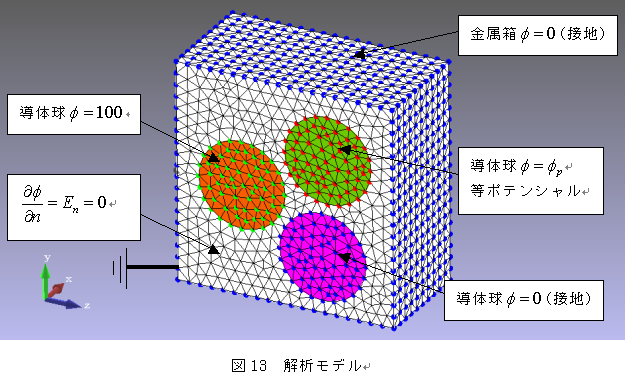



その12 電磁場の境界条件について 株式会社フォトン



北京网信领创科技有限公司 保密室建设 保密设备




3層 垂直入射の反射と透過 電磁波 音波 Notes Jp



Jaxa Repo Nii Ac Jp Action Repository Action Common Download Item Id Item No 1 Attribute Id 31 File No 1




Cna 一种基于低频电磁波的目标定位和追踪系统及方法 Google Patents



Ir Library Osaka U Ac Jp Repo Ouka All Hpc05 027 Pdf



Http Accwww2 Kek Jp Oho Ohotxt Oho 17 Txt Mokuji 17 06 Pdf
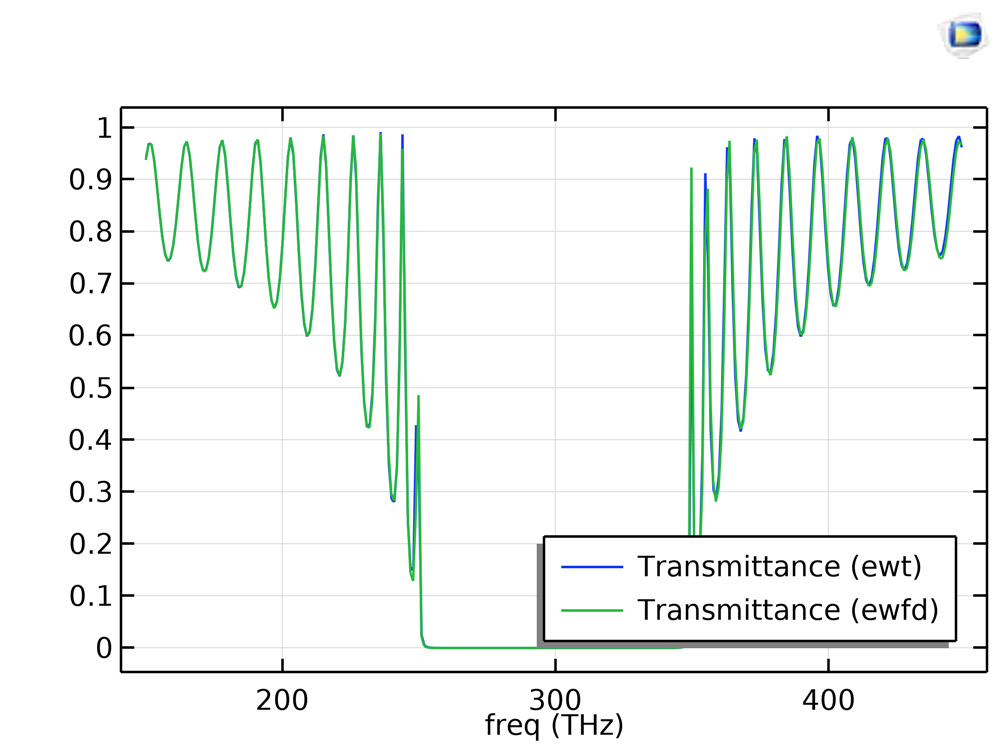



Wave Optics Module Updates Comsol 5 6 Release Highlights



異なる媒質の境界における電磁波と電子波 2 5 境界面における平面波電磁波の時間発展




完全導体境界条件 Ykondo813 S Diary 旧パワエレ Emc日記




Cna 一种基于低频电磁波的目标定位和追踪系统及方法 Google Patents




看看风水师们 勘察风水都用什么工具 网易订阅




綺麗な電磁波 解析 最高の花の画像




全新原装日本oyaide 欧亚德mwa Rc 防电磁波音频信号端子屏蔽盖



Scim Erbi Txt At Master Wwood Scim Github



光の圧力 輻射圧



Http Www Gifu Nct Ac Jp Elec Yamada Denele Denele 11 Pdf



引力与电磁波的爱恨情仇 知乎



異なる媒質の境界における電磁波と電子波 2 2 電磁波に対する透過係数と反射係数の導出




電磁気学 Electromagnetics 6 30講義分 電磁波の反射と透過 山田 博仁 Ppt Download
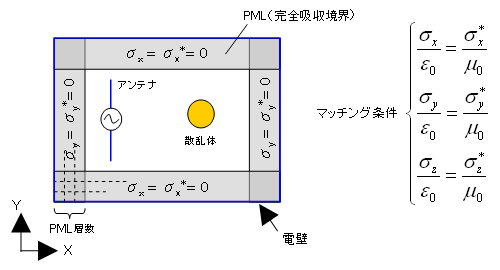



Magna Tdm 特徴 完全吸収境界 Pml により無限空間の扱いが可能



Paper




Cna 一种基于低频电磁波的目标定位和追踪系统及方法 Google Patents
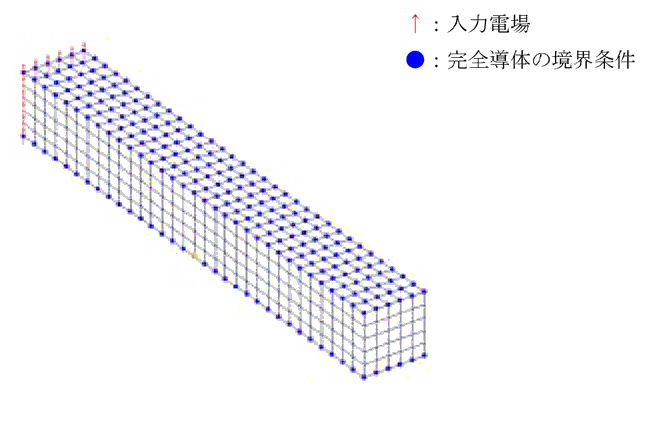



スライドインタフェースを用いた平行平板内の電磁波解析 株式会社フォトン




電磁気学28 電界と電束密度の境界条件とは Youtube




電磁波解析において外部境界での不要な反射を防ぐ方法 計測と制御とcaeソフトウェアの計測エンジニアリングシステム株式会社



高端窗膜制造的三种 神 器 自由微信 Freewechat



電磁波の境界条件について Http Cobalt Cneas Toh Yahoo 知恵袋




電磁気学c Electromagnetics C 5 22講義分 電磁波の反射と透過 山田 博仁 Ppt Download



Emc与emi技术与器件资讯 电子发烧友网
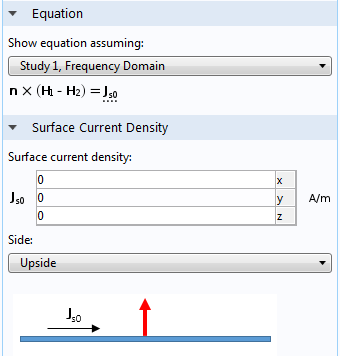



波動光学モジュール Comsol 5 1 リリースハイライト
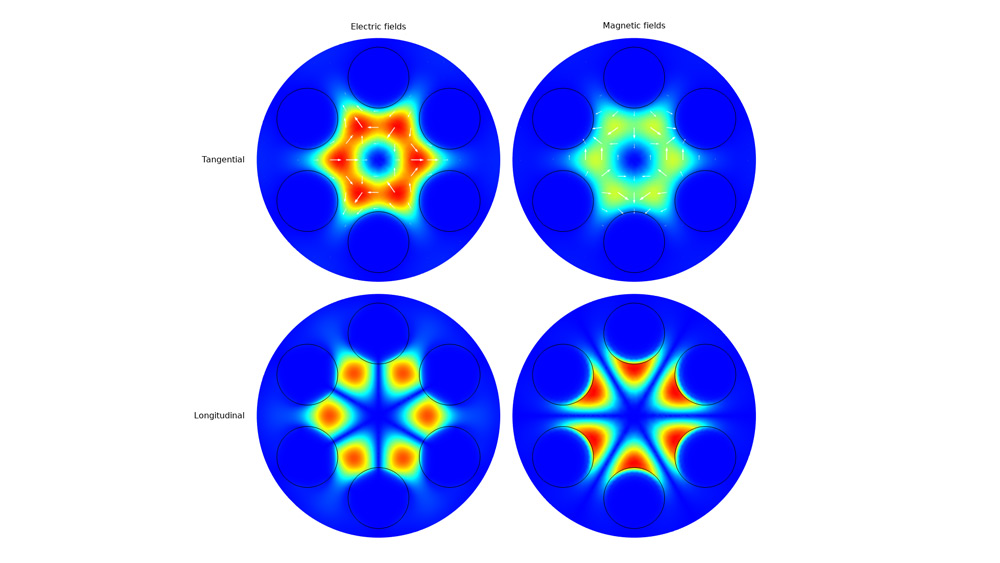



Wave Optics Module Updates Comsol 5 6 Release Highlights



Ppt 電磁気学 C Powerpoint Presentation Free Download Id



電磁気学 Electromagnetics 6 講義分 共振器と導波路 山田 博仁 Ppt Download



引力与电磁波的爱恨情仇 知乎



電磁波の完全導体の境界条件についての質問です 境界面で Yahoo 知恵袋
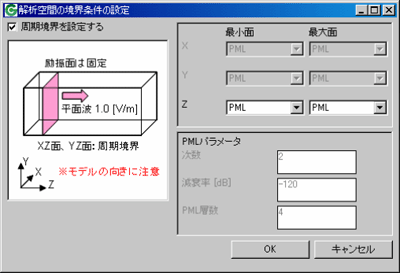



Magna Tdm 特徴 周期構造物に対して周期境界条件の適用が可能



光の圧力 輻射圧
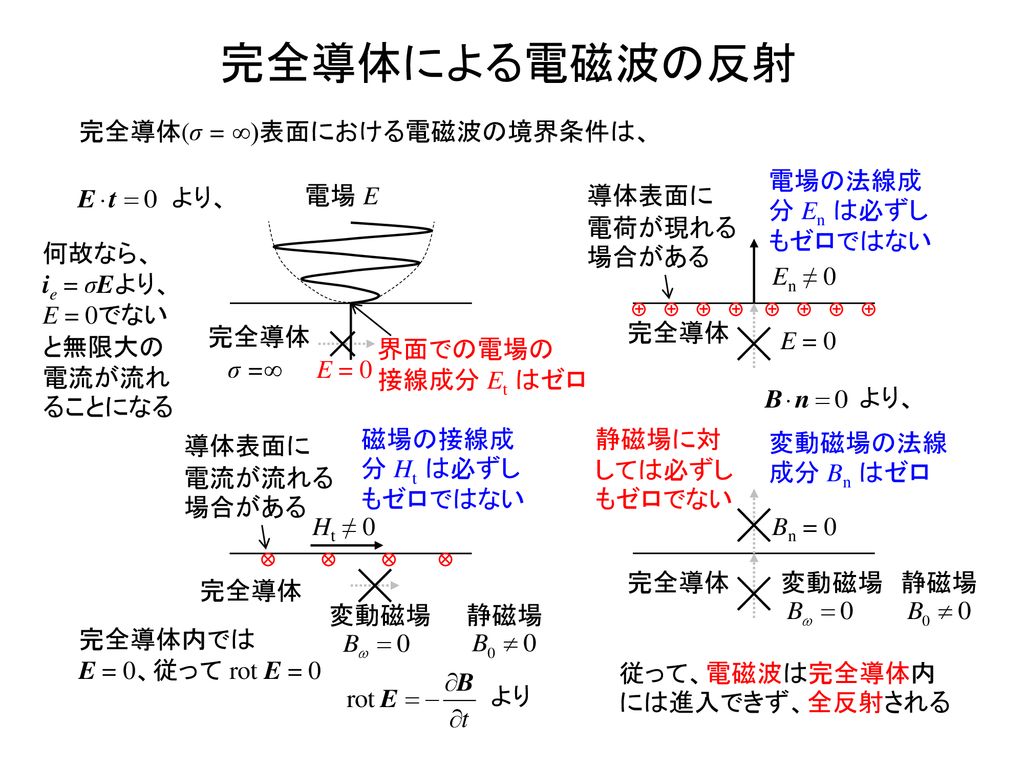



電磁気学c Electromagnetics C 6 24講義分 共振器と導波路 山田 博仁 Ppt Download



电磁学的发展简史下载 Word模板 爱问共享资料




Fdtd法の解説ページをリニューアルしました 株式会社科学技術研究所




日本yahoo拍賣 樂淘letao代購代標第一品牌 振動及び波動末岡清一昭和23年 単振動 多自由度の振動 連続体の振動 電気振動 回析 干渉 音波 水波 電磁波 物質波




波動光学モジュール Comsol 5 1 リリースハイライト
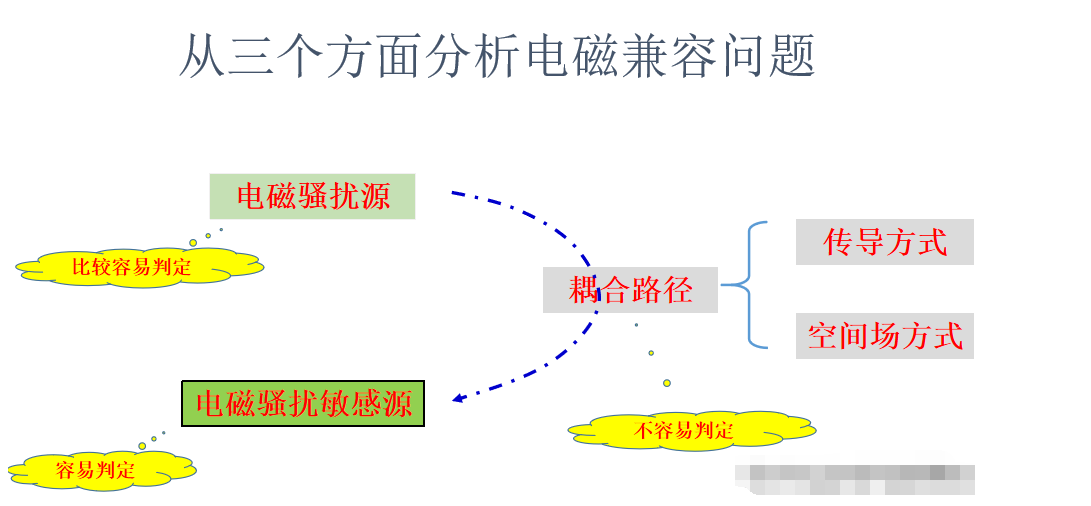



Emc与emi技术与器件资讯 电子发烧友网



改运就是扬升频率 意识
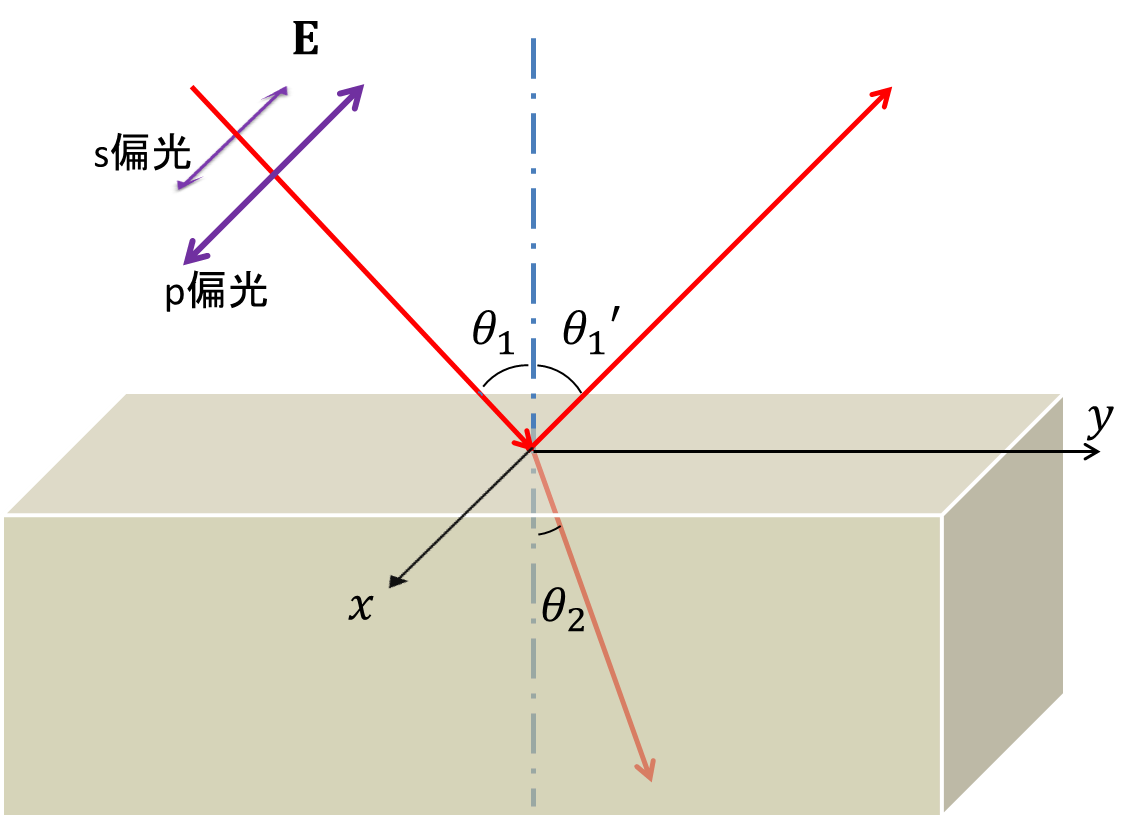



物理とか 偏光と境界条件 反射 屈折の法則
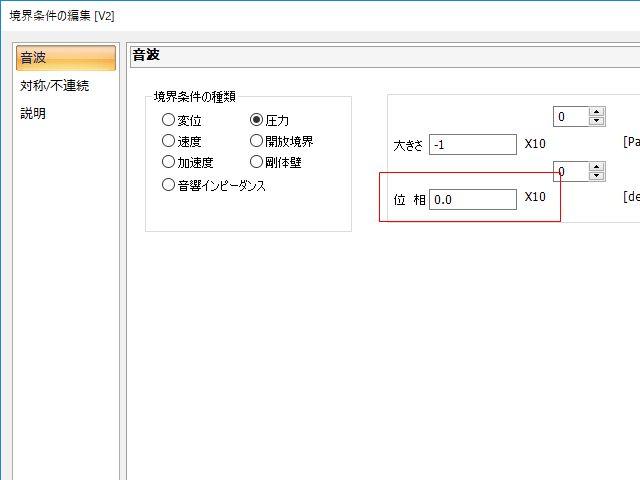



境界条件 ムラタソフトウェアブログ




解析シミュレーションソフトfemtet のバージョンアップについて 村田製作所



励振源 境界条件 収束判定 解析の実効値 株式会社科学技術研究所




通过python进行的科学 技术计算 利用ftcs方法 显式方法 双曲型偏微分方程对一维或二维波动方程进行数值解 码农家园



2



Ppt 電磁気学 C Powerpoint Presentation Free Download Id




信息传递知识点总结下载 Word模板 爱问共享资料



引力与电磁波的爱恨情仇 知乎



0 件のコメント:
コメントを投稿